Poisson process and exponential decay

March 17, 2024

GoLuckyRyan Basic Leave a comment

How does a Poisson process generate the exponential decay?

The exponential decay is derived by

\displaystyle \frac{dN}{dt} = - k N \rightarrow N(t) = N_0 \exp\left(-kt\right) = N_0 2^{- t / \tau}, ~ k = \frac{\log(2)}{\tau}

which means the rate of the loss of the number of nuclei is proportional to the number of nuclei. and \tau is the half-life.

This is a phenomenological and macroscopic equation that tells us nothing about an individual decay.

Can we have a microscopic derivation that, assumes the decay of an individual nucleus following a random distribution?

From this post, we derived the distribution for the differences in a list of sequential random numbers. The key idea is the probability of having a decay at exactly time t - \delta t to t, denote as f(t, \delta t) , is

\displaystyle f(t, \delta t) = P(t-\delta t, 0)P(\delta t, 1)

where P(t,k) is the probability of having k decay within (time) length t, which is a Poisson distribution.

\displaystyle P(t, k) = \frac{t^k}{k!} \exp(-t)

\displaystyle f(t, \delta t) = \frac{(t-\delta t)^0}{0!} \exp(-(t-\delta t)) \frac{\delta t}{1!} \exp(-\delta t) = \exp(-t) \delta t

Now, the total probability of all possible decay within time T, assume not more than 1 decay can happen in \delta t ,

\displaystyle F(T) = \sum_{\delta t \rightarrow 0}^{t < T} f(t, \delta t) = \int_0^{T} \exp(-t) dt = 1- \exp(-T)

Thus, the number of nucleus not decay or survived within time T is

\displaystyle N(t) = N_0 (1 - F(t)) = N_0 \exp(-t) = N_0 2^{-t / \tau}

Radioactivity and Number of Isotopes

March 16, 2024

GoLuckyRyan Basic Leave a comment

Suppose the radioisotope has half-life of \tau and initial number of N_0 , the number of isotopes at give time is

\displaystyle N(t) = N_0 2^{-\frac{t}{\tau}}

The number of decay at a given time, measured with a time period \Delta t is

\displaystyle D(t, \Delta t) = N(t - \Delta t) - N(t)

The rate of number of decay at a given time is

\displaystyle R(t) = \lim_{\Delta t \rightarrow 0} \frac{N(t- \Delta t) - N(t)}{\Delta t} = - N'(t) = \frac{\log2}{\tau} N_0 2^{-\frac{t}{\tau}} = \frac{\log2}{\tau} N(t)

or

\displaystyle N(t) = \frac{\tau}{\log2} R(t)

This, the rate of number of decay is always proportional to the number of radioactive isotopes, therefore, by measuring the radioactivity, the number of radioactive isotopes can be deduced.

For example, suppose we have a sample of tritium with half live of 3.89 \times 10^8 sec. When we measure the sample, we got 100 beta decay in 1 min, that means, the radioactivity is 1.67 decay per second. Therefore the number of isotopes is 9.14 \times 10^8 tritium. Notice that, this number is the number of isotopes at the end of measurement.

For very short half-life, say, few mili-sec, if we collect the number of decay in a few seconds, the number of isotopes changed a lot and the simple ratio \frac{\tau}{\log2} is no longer accurate.

\displaystyle \frac{D(t, \Delta t)}{N(t)} = \frac{N(t - \Delta t) - N(t)}{N(t)} = 2^{\frac{\Delta t}{\tau}} - 1

and

\displaystyle \lim_{\tau \rightarrow \infty} \left( 2^{\frac{\Delta t}{\tau}} - 1 \right) \frac{\tau}{\log 2} = 1

Transform Hamiltonian in rotating frame

March 15, 2024

GoLuckyRyan Basic Leave a comment

I revisit the NMR theory and technical stuff. Doing a 90 degrees flip and measure the Free Induction Decay (FID) signal. The NMR theory is simple, under a magnetic field, the proton spin is precessing at the Larmor frequency, but the spin aligns with the field (alone the z-axis) and the change of the magnetic field on the x-y plane is very weak. To increase the change of the magnetic field, we can flip the spin 90 degrees, make it precesses on the x-y plane and maximize the change of the magnetic field. With the change of the magnetic field induct electric field and voltage on a coil (on the x-axis for example), an signal can be detected at the Larmor frequency. Since the spin will graduate align itself back to the z-axis and so the signal will decay. The technique to flip the spin is called Nuclear Magnetic Resonance. I made a very clumsy note on that many years ago in this pdf.

In order to flip the spin, we need to apply a rotating field with frequency \Omega, in the rotating frame created by the rotating field, an inducted field is created alone the negative z-axis as the world is rotating around (in an opposite direction), and also, a constant field points along the rotating x-axis. When the induced field in the rotating frame can cancel the external magnetic field, the over all effective magnetic field would be the one along the rotating x-axis. Since nuclear spin was on the z-axis, and since switch on of the rotating field, it feels a net magnetic field along the rotating x-axis and start to precess around it. If the rotating field switch off at the time that the spin precesses on the x-y plan, a 90 degree flip is done.

Mathematically, the Hamiltonian a spin under and external magnetic field is

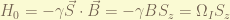
\displaystyle H_0 = -\gamma \vec{S} \cdot \vec{B} = -\gamma B S_z = \Omega_I S_z

where \gamma = \frac{e g_p}{2 m_p} = g_p \frac{\mu_p}{ \hbar } = 42.577~\textrm{MHz}/\textrm{T} is the gyromagnetic ratio of proton, in which g_p is the g-factor of proton and \mu_p is the proton magneton. The Larmor frequency is \Omega_I = -\gamma B .

with a oscillating magnetic field (which is effectively combination of a right-hand and left-hand rotating field), the Hamiltonian is

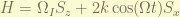
\displaystyle H = \Omega_I S_z + 2k \cos(\Omega t) S_x

The factor k represent the strength of the rotating field. The factor of 2 will comes in handy later. In order to change to the rotating frame, suppose the Lab wavefunction is \phi, the rotating frame wavefunction is \phi_R = \exp(i\Omega t S_z) \phi , the rotating frame Hamiltonian must satisfy

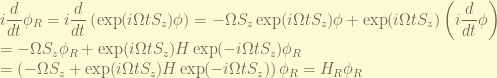
\displaystyle i \frac{d}{dt} \phi_R = i \frac{d}{dt} \left( \exp(i\Omega t S_z) \phi \right) = - \Omega S_z \exp(i\Omega t S_z) \phi + \exp(i\Omega t S_z) \left( i \frac{d}{dt} \phi \right) \\ = - \Omega S_z \phi_R + \exp(i\Omega t S_z) H \exp(-i\Omega t S_z) \phi_R \\ = \left( - \Omega S_z + \exp(i\Omega t S_z) H \exp(-i\Omega t S_z) \right) \phi_R = H_R \phi_R

Thus,

\displaystyle H_R = ( \Omega_I - \Omega) S_z + 2k \cos(\Omega t) \exp(i\Omega t S_z) S_x\exp(-i\Omega t S_z) \\=(\Omega_I - \Omega) S_z + 2k \cos(\Omega t) ( \cos(\Omega t) S_x - \sin(\Omega t )S_y) \\=(\Omega_I - \Omega) S_z + k S_x + k \left( \cos(2 \Omega t) S_x - \sin(2\Omega t )S_y \right) \\= (\Omega_I - \Omega) S_z + k S_x

We can drop the last time dependence terms, because it oscillate at twice of the frequency of the rotating frame, that, in average, the contribution is averaged out. And the Hamiltonian is as expected as our early discussion. an induced field - \Omega S_z along the z-axis, and constant field along the x-axis.

The strength of the oscillating field k has a meaning of rotational frequency. If we apply the field so that T = \pi /4 /k and \Omega = \Omega_I, this will rotate the spin 90 degree and give a maximum reading from the NRM coil. The challenge is that, the actual value of k = -\gamma B_{osc} depends on the effective oscillating magnetic field strength B_{osc}, which depends on the power transfer from the source to the NMR coil, the impedance matching from the coil to the source, also the resonance frequency of the chamber. Some these factors are hard to measure and often, the 90 degree spin flip is achieved by trials and errors until the maximum FID is obtained.