the angular momentum has 2 kinds – orbital angular momentum  , which is caused by a charged particle executing orbital motion, since there are 3 dimension space. and spin
, which is caused by a charged particle executing orbital motion, since there are 3 dimension space. and spin 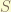 , which is an internal degree of freedom to let particle “orbiting” at there.
, which is an internal degree of freedom to let particle “orbiting” at there.
thus, a general quantum state for a particle should not just for the spatial part and the time part. but also the spin, since a complete state should contains all degree of freedom.
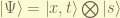
when we “add” the orbital angular momentum and the spin together, actually, we are doing:

where the 1 with L is the identity of the spin-space and the 1 with S is the identity of the 3-D space.
the above was discussed on J.J. Sakurai’s book.
the mathematics of  and
and 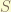 are completely the same at rotation operator.
are completely the same at rotation operator.
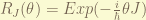
where 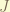 can be either
can be either  or
or 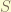 .
.
the  can only have effect on spatial state while
can only have effect on spatial state while 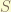 can only have effect on the spin-state. i.e:
can only have effect on the spin-state. i.e:
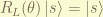
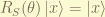
the 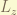 can only have integral value but
can only have integral value but  can be both half-integral and integral. the half-integral value of
can be both half-integral and integral. the half-integral value of  makes the spin-state have to rotate 2 cycles in order to be the same again.
makes the spin-state have to rotate 2 cycles in order to be the same again.
thus, if the different of  and
and 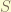 is just man-made. The degree of freedom in the spin-space is actually by some real geometry on higher dimension. and actually, the orbital angular momentum can change the spin state:
is just man-made. The degree of freedom in the spin-space is actually by some real geometry on higher dimension. and actually, the orbital angular momentum can change the spin state:

but the effect is so small and

but the c is very small, but if we can rotate the state for a very large angle, the effect of it can be seen by compare to the rotation by spin.
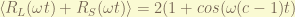
the experiment can be done as follow. we apply a rotating magnetic field at the same frequency as the Larmor frequency. at a very low temperature, the spin was isolated and  and
and  is equal to
is equal to 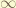 . the different in the c will come up at very long time measurement and it exhibit a interference pattern.
. the different in the c will come up at very long time measurement and it exhibit a interference pattern.
if  is a complex number, it will cause a decay, and it will be reflected in the interference pattern.
is a complex number, it will cause a decay, and it will be reflected in the interference pattern.
if we find out this c, then we can reveal the other spacial dimension!
___________________________________
the problem is. How can we act the orbital angular momentum on the spin with out the effect of spin angular momentum? since L and S always coupled.
one possibility is make the S zero. in the system of electron and positron. the total spin is zero.
another possibility is act the S on the spatial part. and this will change the energy level.
__________________________________
an more fundamental problem is, why L and S commute? the possible of writing this
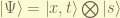
is due to the operators are commute to each other. by why?
if we break down the L in to position operator x and momentum operator p, the question becomes, why x and S commute or p and S commute?
![[x,S]=0 ?](https://s0.wp.com/latex.php?latex=%5Bx%2CS%5D%3D0+%3F+&bg=fafad3&fg=6f5e4e&s=0&c=20201002)
![[p,S]=0 ?](https://s0.wp.com/latex.php?latex=%5Bp%2CS%5D%3D0+%3F+&bg=fafad3&fg=6f5e4e&s=0&c=20201002)
![[p_x, S_y] \ne 0 ?](https://s0.wp.com/latex.php?latex=%5Bp_x%2C+S_y%5D+%5Cne+0+%3F+&bg=fafad3&fg=6f5e4e&s=0&c=20201002)
i will prove it later.
___________________________________
another problem is, how to evaluate the Poisson bracket? since L and S is not same dimension. may be we can write the eigenket in vector form:

i am not sure.
___________________________________
For any vector operator, it must satisfy following equation, due to rotation symmetry.
![[V_i, J_j] = i \hbar V_k](https://s0.wp.com/latex.php?latex=%5BV_i%2C+J_j%5D+%3D+i+%5Chbar+V_k+&bg=fafad3&fg=6f5e4e&s=0&c=20201002) run in cyclic
run in cyclic
Thus,
where J is rotation operator. but i am not sure is it restricted to real space rotation. any way, spin is a vector operator, thus
$latex [S_x, L_y] = i \hbar S_z = – [S_y, L_x] $
so, L, S is not commute.
,
,
is magnetic dipole moment (MDM). It is
.
is the g-factor,
is magneton, and
is the total spin, which has a intrinsic factor
inside.
is gyromegnetic ratio.
,
, thus, we can see the
has unit of frequency over Tesla.
. The MDM is,
.
,
.
is not convenient for experiment. The gyromagnetic ratio usually divided by
,
.
. However, the g-factor for
is difference from that for
. Thus, the MDM is not parallel to total spin. We have to use Landé Formula,
,
