Runge-Kutta | Nuclear Physics 101

Variational method for Woods-Saxon potential

August 31, 2021

GoLuckyRyan Basic Hankel, Runge-Kutta, Schrödinger equation, spherical Bessel, Variational method Leave a comment

In the past, we solved the radial wavefunction for the Woods-Saxon potential by Runge-Kutta method. But there is another method based on linear algebra, that all wave function can be expanded as a linear combination of a set of basis. In here, we use a free wave as basis, which is the spherical Bessel function.

to be annoying due to my poor memory , lets state the Schrödinger equation again,

$\displaystyle \left( -\frac{\hbar^2}{2m}\nabla^2 + V(r) \right)\Psi = E\Psi$

Separating the radial part

$\displaystyle \left( -\frac{\hbar^2}{2m} \frac{1}{r^2} \left( \frac{d}{dr} r^2 \frac{d}{dr} \right) +\frac{\hbar^2}{2m} \frac{l(l+1)}{r^2}+ V(r) \right) R(r) = E R(r)$

replace $R(r) = u(r) /r$

$\displaystyle \frac{1}{r^2} \left( \frac{d}{dr} r^2 \frac{d}{dr} \right) \frac{u(r)}{r} = \frac{1}{r}\frac{d^2}{dr^2} u(r)$

$\displaystyle \left( -\frac{\hbar^2}{2m} \frac{d^2}{dr^2} + \frac{\hbar^2}{2m} \frac{l(l+1)}{r^2} + V(r) \right) u(r) = E u(r)$

simplify

$\displaystyle \left( \frac{d^2}{dr^2} - \frac{l(l+1)}{r^2} - \frac{2m}{\hbar^2} V(r) \right) u(r) = -\frac{2m}{\hbar^2}E u(r)$

We can define a “free wave” Hamiltonian as

$\displaystyle \left( \frac{d^2}{dr^2} - \frac{l(l+1)}{r^2} \right) u(r) = H_0 u(r) = -k^2 u(r)$

In this post, we explored the orthogonality of the the Riccati-Bessel function, and it is the eigen state for $H_0$ with eigenvalue of $-k_n^2$ .

$\displaystyle b_k(r) = \sqrt{\frac{2}{pi}} \hat{j_l}\left(k r\right), ~~~ H_0 b_k(r) = -k^2 b_k(r)$

$\displaystyle \left< b_k | b_k' \right> = \delta(k-k')$

Thus, the Riccati-Bessel function can be served as the set of basis functions that span the whole space.

The total Hamiltonian is then

$\displaystyle \left( -\frac{\hbar^2}{2m} \frac{d^2}{dr^2} + \frac{\hbar^2}{2m} \frac{l(l+1)}{r^2} + V(r) \right) u(r) \\~~~~~~~~~~~~~~~~= \left( -\frac{\hbar^2}{2m} H_0 + V(r) \right) u(r) = E u(r)$

Since the solution can be expressed as a linear combination of the basis functions, then

$\displaystyle u(r) = \sum_n a_n b_n(r)$

$\displaystyle \left( -\frac{\hbar^2}{2m} H_0 + V(r) \right) \sum_n a_n b_n(r) = E\sum_n a_n b_n(r)$

Multiple $b_m(r)$ and integrate,

$\displaystyle \sum_{n} a_n \left< b_m \left| -\frac{\hbar^2}{2m}H_0 + V(r) \right|b_n \right> = E a_m$

The above is a matrix equation

$\displaystyle \left< -\frac{\hbar^2}{2m} H_0 + V(r) \right> \vec{a} = E \vec{a}, ~~ \vec{a} = (a_1, a_2,... a_N)$

Everything seems OK. But when I test the theory using Mathematica, it fail. For simplicity, we use the s-orbital, and the basis is

$\displaystyle b_n(r) = \sqrt{\frac{2}{\pi}} \sin\left( \frac{2\pi}{a} n r\right)$

The Woods-Saxon parameters are $V_0 = -50 \mbox{MeV}, V_{so} = 22 \mbox{MeV}, R_0 = R_{so} = 4 \mbox{fm}, a_0 = a_{so} = 0.67 \mbox{fm}$ .

Using Runge-Kutta method, the ground state energy is -36.09 MeV, and the wave function is

We set $a = 40~\mbox{fm}$ , and $n = 1, 2, ...., 40$ . The matrix elements is

$\displaystyle \left<n \left| -\frac{\hbar^2}{2m_n}H_0 + V(r) \right| m \right> = \delta_{nm} \frac{\hbar^2 k^2}{2m_n} + \left<V(r) \right>, ~~ k = \frac{2\pi}{a} n$

where $m_n$ is neutron mass.

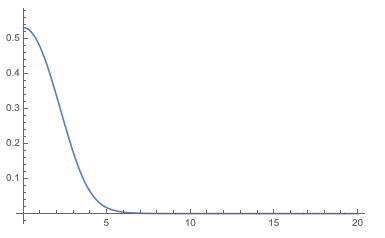
After calculate the matrix, find the eigenvalue and eigenstate. The lowest eigen energy is -465.18 MeV, which indicate something wrong. And the wave function, constructed by the eigenstate look likes

Ground state constructed by basis functions

The shape of the wavefunction looks similar to the correct wavefunction, but narrower and larger amplitude.

The next eigen wave function also look like 1s-orbital. The spectrum of the eigenvalues, which are the eigen energies, has 7 bound states.

I don’t know the problems….

One possible reason could be that the basis function is always $b_n(a) = 0$ , but the real solution is not necessary to be $\psi(a) = 0$ . In fact, the 0s-wave function never be zero except $r= 0$ .

I use the same basis and extract the coefficient,

$\displaystyle \psi(r) \approx \sum_{n}^{40} C_n \frac{\sin(k_n r)}{r}, ~ C_n = \int_0^\infty \psi(r) \sin(k_n r) r dr, ~ k_n = \frac{2\pi}{a}n$

And it can reproduce the original wave function at $r < 10 \mbox{fm}$

Since the basis function is a sine wave and we only sum limited term, the long range oscillation can not be suppressed.

Another possible reason is that the basis is not normalizable. This root at the orthogonality of Bessel function that

$\displaystyle \int_0^\infty J_\nu^2(kx) x dx = \infty$

An-another possible reason is that, the basis is for unbound state. But in this post, we used a not-normalizable, unbounded basis to construct the bound state wave function. It can form the solution correctly at short-range, but it is periodic. This is the nature of series expansion, always periodic.

In this sense, we are also expanding the solution into a series, that the series only produce periodic function, therefore, a correct way to do is using the spherical Hankel transform, which is transform the Schrodinger equation into momentum space.

Runge-Kutta method for coupled ODE

June 23, 2021

GoLuckyRyan Basic Magnetic field, Runge-Kutta Leave a comment

The problem arises when solving the trajectory for a charged particle in 3-D magnetic field and electric field. The Lorentz force is

$\displaystyle \vec{F} = m \frac{d\vec{v}}{dt}= Qe \vec{E} + Qe \vec{v} \times \vec{B}$

This is a second order couple ODEs.

$\displaystyle \frac{d^2\vec{r}}{dt^2}= \frac{Q}{m}e \left(\vec{E}(\vec{r}) + \frac{d\vec{r}}{dt} \times \vec{B}(\vec{r}) \right) = \vec{G}\left(t, \vec{r}, \frac{d\vec{r}}{dt} \right)$

Decompose into the x, y, z coordinate

$\displaystyle x''(t)= \alpha \left(E_x(x, y, z) + y'(t) B_z(x,y,z) - z'(t) B_y(x,y,z) \right) = G_x( t, \vec{r}, \vec{v})$

$\displaystyle y''(t)= \alpha \left(E_y(x, y, z) + z'(t) B_x(x,y,z) - x'(t) B_z(x,y,z) \right) = G_y( t, \vec{r}, \vec{v})$

$\displaystyle z''(t)= \alpha \left(E_z(x, y, z) + x'(t) B_y(x,y,z) - y'(t) B_z(x,y,z) \right) = G_z( t, \vec{r}, \vec{v})$

In Mathematica, the code is

RK23[Gx_Symbol, Gy_Symbol, Gz_Symbol, t0_, r0_, v0_, dt_, nStep_] := 
 Module[{sol, t, r, v, dr, dv},
  sol = Table[{t0 + (i - 1) dt, {0, 0, 0}, {0, 0, 0}}, {i, 1, nStep}];
  sol[[1, 2]] = r0; sol[[1, 3]] = v0;
  dr = Table[{0, 0, 0}, {i, 1, 5}];
  dv = Table[{0, 0, 0}, {i, 1, 5}];
  Table[
   t = sol[[i - 1, 1]];
   r = sol[[i - 1, 2]];
   v = sol[[i - 1, 3]];
   Do[ 
    dr[[j]] = dt (v + parC[[j - 1]] dv[[j - 1]]);
    dv[[j]] = dt {
       Gx[t + parC[[j - 1]] dt, r + parC[[j - 1]] dr[[j - 1]], 
        v + parC[[j - 1]] dv[[j - 1]]],
       Gy[t + parC[[j - 1]] dt, r + parC[[j - 1]] dr[[j - 1]], 
        v + parC[[j - 1]] dv[[j - 1]]],
       Gz[t + parC[[j - 1]] dt, r + parC[[j - 1]] dr[[j - 1]], 
        v + parC[[j - 1]] dv[[j - 1]]]
       };
    , {j, 2, 5}];
   dr[[0]] = Sum[parD[[j - 1]] dr[[j]], {j, 2, 5}];
   dv[[0]] = Sum[parD[[j - 1]] dv[[j]], {j, 2, 5}];
   sol[[i, 2]] = r + dr[[0]];
   sol[[i, 3]] = v + dv[[0]];
   , {i, 2, nStep}];
  sol
  ]

A test field is

$\displaystyle B_x=0, B_y = 0, B_z = \exp\left(- \frac{x^2+y^2}{40} \right) \cos(\sqrt{x^2+y^2}) \cos\left(2\pi\frac{ z}{20}\right)$

We send a proton with velocity 2 units. Here are the trajectories from different positons

using the NDSolve in Mathematica and test on some simple case, I verified the calculation is correct.

Calculation of Woods-Saxon energy levels

March 21, 2019

GoLuckyRyan Basic Runge-Kutta, Woods-Saxon 2 Comments

Hello everyone, I have been very busy lately, working on many things at the same time. Writing experiment proposal, testing a new detector array, flighting with the noise. Coding a program to read digitizer data for real time. Update the analysis code for coming experiments. Update/making some calculation codes, one of them is the calculation of Woods-Saxon energy levels.

Using RK4 method, a 2ndary 1-D differential potential can be solved easily (with some effort).

The Woods-Saxon potential with spin-orbital coupling is:

$\displaystyle H = \frac{P^2}{2m} + V(r) + \frac{1}{r} \frac{d}{dr}V_{so}(r)\langle L\cdot S\rangle$

$\displaystyle V(r) = \frac{V_0 }{1+ \exp{\frac{r-R_0}{a_0}}}$

$\displaystyle V_{so}(r) = \frac{V_{so}}{1+\exp{\frac{r-R_{so}}{a_{so}}}}$

There are 6 parameters, 3 for the central term, 3 for the spin-orbital term.

And the equation is

$\displaystyle H\Psi(r, \theta, \phi) = E \Psi(r, \theta, \phi)$

Since the radial wavefunction has to be zero when it is far away, we can search for energy, such that the wavefunction is close to zero at a certain range. ( this is the only method I know how to practically implemented. I can imagine that, there may be some other method, transform the whole equation with a fixed r and directly solve the energy. Something like least-square method for linear system can be transformed into Matrix formalism and be directly solved. But I don’t know how)

The code is available at github (currently only for neutron).

I also have an excel to solve a single energy. Feel free to leave in comment and I will email it to you.

Phase shift of elastics scattering

September 29, 2016

GoLuckyRyan Basic, theory elastic, Partial wave, phase shift, Runge-Kutta, S-matrix, scattering Leave a comment

I found that the derivation of most “google result” is not clear enough. So here is my derivation. Before process, people may need to review the pervious post.

Most people start from,

$u_l = A( \hat{h}_l^- - S_l \hat{h}_l^+ )$

that annoying me because it is somehow not “natural”. Why there is a “minus” sign? Why the $\hat{h}_l^-$ is the first term? For my self, a more natural way is,

$u_l = a \hat{h}_l^+ + b \hat{h}_l^-$

where $a, b$ are complex numbers, but that is still not so natural, because in numerical calculation, for simplicity, there is no complex number, we only have,

$u_l = \alpha \hat{j}_l + \beta \hat{n}_l$

The first term is alway there as it is the free solution and bounded at $r = 0$ . the second term is caused by the potential.

The goal is to find a solution take the form

$\displaystyle \psi = A \left( e^{i \vec{k} \cdot \vec{r}} + f(\theta) \frac{e^{ikr}}{r} \right)$

where the first term is free wave and the second term is scattered wave. The solution for elastics scattering is

$\displaystyle \psi = \sum C_l P_l (\cos\theta) \frac{u_l}{kr} \rightarrow \sum C_l P_l(\cos\theta) (\alpha \hat{j}_l + \beta \hat{n}_l)$

we used the substitution,

$\displaystyle R_l(r) = \frac{u_l(\rho)}{\rho}, \rho = kr$ .

The radial function can be solved using Rungu-Kutta method on the equation,

$\displaystyle \frac{d^2}{d\rho^2} u_l = \frac{2 m_\mu}{\hbar^2} (V-E) u_l + \frac{l(l+1)}{\rho^2}$

and the solution of $u_l$ at far away is,

$u_l \rightarrow \alpha \hat{j}_l + \beta \hat{n}_l$ .

the arrow means $r \rightarrow \infty$ . So, the problem is how to rewrite the solution. In the way, we will see how the phase shift or the S-matrix was found.

The free solution is the spherical wave,

$\displaystyle e^{i \vec{k} \cdot \vec{r}} = \sum_l (2l+1) i^l P_l(\cos\theta) j_l(kr)$

The spherical Bessel function $j_l(kr)$ cna be express as Heankel function

$h_l^{\pm} = n_l \pm i j_l \rightarrow e^{\pm i (kr - l \frac{\pi}{2})}$

The $+$ sign is outgoing wave.

$\displaystyle u_l \rightarrow (\alpha \hat{j}_l + \beta \hat{n}_l)$

$\displaystyle = \frac{\alpha}{2i} (\hat{h}_l^{+} - \hat{h}_l^{-}) + \frac{\beta}{2}(\hat{h}_l^{+} + \hat{h}_l^{-})$

$\displaystyle = \frac{\alpha - i \beta}{2i} (\hat{h}_l^{+} - \hat{h}_l^{-}) + \beta \hat{h}_l^{+}$

$\displaystyle = (\alpha - i \beta ) \left( \frac{\hat{h}_l^+ - \hat{h}_l^-}{2i} + \frac{\beta}{\alpha - i \beta} \hat{h}_l^+\right)$

$\displaystyle = (\alpha - i \beta ) \left( \hat{j}_l + \frac{\beta}{\alpha - i \beta} \hat{h}_l^+\right)$

Since the $u_l$ should be normalized, we can se $\alpha = \cos \delta$ and $\beta = \sin\delta$ .

$\displaystyle \frac{\beta}{\alpha - i \beta } = \sin(\delta) e^{i\delta}$

We put $u_l$ back

$\displaystyle \psi \rightarrow \sum_l C_l P_l (cos\theta)(\alpha - i \beta ) \left( \hat{j}_l + \sin(\delta) e^{i\delta} \hat{h}_l^+\right)$

By setting

$\displaystyle C_l = A i^l \frac{2l+1}{\alpha - i \beta}$ ,

we have the first term is the free wave function. In the second term, $\hat{h}_l^+ \rightarrow e^{i(kr - l \frac{\pi}{2}}) / kr$ . Notice that

$e^{i l \frac{\pi}{2}} = i^{-l}$

That cancel the $i^l$ term in $C_l$ . And we have

$\displaystyle f(\theta) = \sum (2l+1) P_l (\cos\theta) \frac{\sin(\delta) e^{i\delta}}{k}$

some people will write the $u_l$ as $\hat{h}_l^{\pm}$ and the S-matrix,

$\displaystyle u_l = \frac{\alpha + i \beta} {2i} \hat{h}_l^+ - \frac{\alpha - i \beta}{2i} \hat{h}_l^-$

$\displaystyle = -\frac{\alpha - i \beta}{2i} \left( \hat{h}_l^- - \frac{\alpha + i \beta}{\alpha - i \beta} \hat{h}_l^+ \right)$

$\displaystyle = A' (\hat{h}_l^- - S_l \hat{h}_l^+)$

where

$\displaystyle S_l =\frac{\alpha + i \beta}{\alpha - i \beta} = e^{2i\delta}$ .

Remember that this is the S-matrix for elastics scattering.

Solving radial SE numerically

July 8, 2016

GoLuckyRyan Basic, Math, theory bound state, Eigen System, Laplacian, Runge-Kutta, scattering, Schrödinger equation 4 Comments

The time-independent Schrödinger equation is

$\displaystyle (-\frac{\hbar^2}{2m}\nabla^2 + V ) \Psi = E \Psi$

Using the Laplacian in spherical coordinate. and Set $\Psi = R Y$

$\displaystyle \nabla^2 R Y - \frac{2m}{\hbar^2}(V-E) R Y = 0$

$\displaystyle \nabla^2 = \frac{1}{r^2}\frac{d}{dr}(r^2 \frac{d}{dr}) - \frac{1}{r^2} L^2$

The angular part,

$L^2 Y = l(l+1) Y$

The radial part,

$\displaystyle \frac{d}{dr}(r^2\frac{dR}{dr}) - l(l+1)R - \frac{2mr^2}{\hbar^2}(V-E) R = 0$

To simplify the first term,

$\displaystyle R = \frac{u}{r}$

$\displaystyle \frac{d}{dr}(r^2 \frac{dR}{dr})= r \frac{d^2u}{dr^2}$

A more easy form of the radial function is,

$\displaystyle \frac{d^2u}{dr^2} + \frac{l(l+1)}{r^2} u - \frac{2m}{\hbar^2} (V-E) u = 0$

The effective potential $U$

$U = V + \frac{\hbar^2}{m} \frac{l(l+1)}{r^2}$

$\displaystyle \frac{d^2u}{dr^2} + \frac{2m}{\hbar^2} (E - U) u = 0$

We can use Rungu-Kutta method to numerically solve the equation.

The initial condition of $u$ has to be 0. (home work)

I used excel to calculate a scattered state of L = 0 of energy 30 MeV. The potential is a Wood-Saxon of depth 50 MeV, radius 3.5 fm, diffusiveness 0.8 fm.

Another example if bound state of L = 0. I have to search for the energy, so that the wavefunction is flat at large distance. The outermost eigen energy is -7.27 MeV. From the radial function, we know it is a 2s orbit.

Special Runge-Kutta method for any order ODE

June 18, 2016

GoLuckyRyan Basic Runge-Kutta Leave a comment

The central piece of Runge-Kutta method is the approximation of the incensement of the function. In 1st order ODE,

$\dot{x} = f(t,x), \dot{x}(t_0) = x_0$

In a special case of Runge-Kutta of order 4 (RK4), there are 2 array $b_i$ and $c_i$ , so that

$dt = h, dx = \sum\limits_{i=1}^{4} b_i dx_i$

$dx_i = h f(t+ c_i dx, x+c_i dx_{i-1})$

where $c_i$ is ranging from 0 to 1, $\sum\limits_{i=1}^{4} b_i =1$ .

In RK4,

$c = (0, \frac{1}{2}, \frac{1}{2}, 1)$

$b = \frac{1}{6}(1,2,2,1)$

The $c_1 = 0$ is a must, otherwise, we have to define $dy_0$ . There should be some methods to obtain an optimum values for $c$ and $b$ , but I don’t know.

In Mathematica,

RK1[G_Symbol, t0_, x0_, dt_, nStep_] := Module[{sol, t, x, dx},
  sol = Table[{t0 + (i - 1) dt, 0}, {i, 1, nStep}]; sol[[1, 2]] = x0;
  dx = Table[0, {i, 1, 5}];
  Table[
   t = sol[[i - 1, 1]];
   x = sol[[i - 1, 2]];
   Do[ dx[[j]] = 
     dt G[t + parC[[j - 1]] dt, x + parC[[j - 1]] dx[[j - 1]]], {j, 2,
      5}];
   dx[[0]] = Sum[parD[[j - 1]] dx[[j]], {j, 2, 5}];
   sol[[i, 2]] = x + dx[[0]] ;
   , {i, 2, nStep}];
  sol
  ]

For 2nd order ODE

$\displaystyle \frac{d^2y}{dx^2} + a \frac{dy}{dx} = f(x,y), \\y(x_0) = y_0, \\ \frac{dy}{dx}|_{x_0} = z_0$

change to

$\displaystyle \frac{dy}{dx} = z, \frac{dz}{dx}=F(x,y,z)$

These equation are the similar 1st order ODEs.

$\displaystyle dx = h, \\dy = \sum\limits_{i=1}^{4} b_i dy_i, \\dz = \sum\limits_{i=1}^{4} b_i dz_i$

, where

$\displaystyle dy_i = h( z+ c_i dz_{i-1})$

$\displaystyle dz_i = h F(x+ c_i dx, y+c_i dy_{i-1}, z+c_i dz_{i-1})$

$\displaystyle dy_0 = dz_0 = 0$

The $dy_i$ is using $dz_i$

$x_{n+1} = x_n + dx$

$y_{n+1} = y_n + dy$

$z_{n+1} = z_n + dz$

In Mathematica

RK2[G_Symbol, t0_, x0_, v0_, dt_, nStep_] := 
 Module[{sol, t, x, v, dx, dv},
  sol = Table[{t0 + (i - 1) dt, 0, 0}, {i, 1, nStep}]; 
  sol[[1, 2]] = x0; sol[[1, 3]] = v0;
  dx = Table[0, {i, 1, 5}];
  dv = Table[0, {i, 1, 5}];
  Table[
   t = sol[[i - 1, 1]];
   x = sol[[i - 1, 2]];
   v = sol[[i - 1, 3]];
   Do[ 
    dx[[j]] = dt (v + parC[[j - 1]] dv[[j - 1]]);
    dv[[j]] = 
     dt G[t + parC[[j - 1]] dt, x + parC[[j - 1]] dx[[j - 1]], 
       v + parC[[j - 1]] dv[[j - 1]]];
    , {j, 2, 5}];
   dx[[0]] = Sum[parD[[j - 1]] dx[[j]], {j, 2, 5}];
   dv[[0]] = Sum[parD[[j - 1]] dv[[j]], {j, 2, 5}];
   sol[[i, 2]] = x + dx[[0]];
   sol[[i, 3]] = v + dv[[0]];
   , {i, 2, nStep}];
  sol
  ]

This can be generalized to any order ODE by decoupling the ODE into

$\frac{dy}{dx} = x,..., \frac{du}{dx}=F(x,y,...,u)$

the equation for $du_i$ is

$du_i = h F(x+ c_i dx, y+c_i dy_{i-1}, z+c_i dz_{i-1}, ...., u+ c_i du_{i-1})$

And for all the intermediate variable $y, z, w,.... = O^{(k)}$

$dO_i^{(k+1)} = h( O^{(k)} + c_i dO_{i-1}^{(k)})$

Very short introduction to Partial-wave expansion of scattering wave function

February 26, 2016

GoLuckyRyan Basic, nuclear, Scattering, theory Bessel function, Coulomb, Cross section, Legendre polynomial, Partial wave, phase shift, radio, Runge-Kutta, S-matrix, scattering, scattering amplitude Leave a comment

In a scattering problem, the main objective is solving the Schrödinger equation

$H\psi=(K+V)\psi=E\psi$

where H is the total Hamiltonian of the scattering system in the center of momentum, K is the kinetic energy and V is the potential energy. We seek for a solution $\psi$ ,

$\displaystyle \psi_{k}^{+}(r)=e^{i\vec{k}\cdot \vec{r}}+f(\theta)\frac{e^{ikr}}{kr}$

The solution can be decomposed

$\displaystyle \psi_{k}^{+}(r)=R_{l}(k,r)Y_{lm}(\theta,\phi)=\frac{u_{l}(k,r)}{kr}Y_{lm}(\theta,\phi)$

The solution of $u_{l}(k,r)$ can be solve by Runge-Kutta method on the pdf

$\displaystyle \left(\frac{d^2}{d\rho^2} + 1 - \frac{l(l+1)}{\rho^2} \right)u_{l}(k,\rho)=U(\rho)u_{l}(k,\rho)$

where $\rho=kr, k=\sqrt{2\mu E}/\hbar, \mu=(m_1+m_2)/(m_1 m_2)$ and $U=V/E$ .

For $U = 0$ , the solution of $u_l$ is

$\displaystyle u_{l}(k,r)=\hat{j}_l(\rho) \xrightarrow{r\rightarrow \infty} \sin(r') = \frac{e^{ir'}-e^{-ir'}}{2i}$

where $r' = kr-l\pi/2$ and $\hat{j}_l$ is the Riccati-Bessel function. The free wave function is

$\displaystyle \phi_k(r)=e^{i\vec{k}\cdot\vec{r}}=\sum\limits_{l=0} P_l(\cos(\theta)) \frac{2l+1}{2ikr}i^l (e^{ir'}-e^{-ir'})$

where $P_l(x)$ is the Legendre polynomial.

Note that, if we have Coulomb potential, we need to use the Coulomb wave instead of free wave, because the range of coulomb force is infinity.

For $U\neq 0$ , the solution of $u_l(r<R)$ can be found by Runge-Kutta method, where R is a sufficiency large that the potential $V$ is effectively equal to 0. The solution of $u_l(r>R)$ is shifted