transfer reaction | Nuclear Physics 101

PRL paper

February 13, 2020

GoLuckyRyan Basic 207Hg, paper reading, transfer reaction Leave a comment

Haha!

https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.124.062502

Here are two news for this subject.

https://phys.org/news/2020-02-isolde-unexplored-region-nuclear-exotic.html

https://home.cern/news/news/physics/isolde-steps-unexplored-region-nuclear-chart

The experiment is simple and elegant. A neutron is put on top of 206Hg, which has N=126 and magic. This extra neutron will populate the next major shell ( N > 126). From the energy and angular distribution measured. We can identify the single-particle energy level, the orbital angular momentum. With the help of DWBA calculation, the occupation or the spectroscopic number can be extracted.

We deduced the single-particle energies and compared with Woods-Saxon calculation. Together with the 209Pb single particle energies. We extrapolating the single-particle energy to the neutron-dripline, where the r-process for heavy nuclear synthesis expected to take place. The result agree with most of the present theoretical calculations. In other word, the present theoretical calculations are seem to be fine.

HELIOS – an inverse problem

October 31, 2018

GoLuckyRyan Basic 2-body reaction, HELIOS, transfer reaction Leave a comment

When give incident energy, the transfer reaction (or 2-body reaction in general) in a magnetic field is a transform:

$\displaystyle \begin{pmatrix} E_x \\ \theta_{cm} \end{pmatrix} \rightarrow \begin{pmatrix} E \\ z \end{pmatrix}$

We already give the constant $E_x$ line and constant $\theta_{cm}$ line in previous posts. Now, we study an inverse problem that, given the energy and z-position, or a point on the EZ plot, what is the excitation energy and center of mass angle?

The solution is

$\displaystyle \begin{pmatrix} E_x \\ \theta_{cm} \end{pmatrix} = \begin{pmatrix} - m_B + \sqrt{E_t^2 + m_b^2 - 2\gamma E_t (E - \alpha \beta z)} \\ \frac{\gamma \beta E - \alpha \gamma z}{ \sqrt{\gamma^2 (E-\alpha \beta z)^2 - m_b^2}} \end{pmatrix}$

The above solution is for infinite detector, which is not really practical.

Assume the rotation radius is much larger than the detector size $a$ . The coupled equations are:

$\displaystyle E = \gamma E_{cm} - \gamma \beta p \cos(\theta_{cm})$

$\displaystyle \alpha \beta \gamma z = (\gamma E - E_{cm})\left( 1- \frac{1}{2\pi} \frac{a}{\rho} \right)$

$\displaystyle \rho = \frac{ p \sin(\theta_{cm}} {2\pi a}$

eliminate $\theta_{cm}$ ,

$\displaystyle \alpha \beta \gamma z = (\gamma E - E_{cm})\left( 1- \frac{\alpha \gamma \beta a}{\sqrt{2\gamma E E_{cm} - E^2 - m^2 \gamma^2 - p^2}} \right)$

Since $E_{cm}^2 = m^2 + k^2$

Change of variable

$\displaystyle k \rightarrow m \tan(x) , 0 < x < \pi/2$

$\displaystyle z = \frac{\gamma E - m \sec(x)}{\alpha \beta \gamma }\left( 1- \frac{\alpha \gamma \beta a}{\sqrt{2\gamma E m \sec(x) - E^2 - m^2 \gamma^2 - m^2 \tan^2(x)}} \right)$

The square root can be rearranged as,

$\displaystyle 2\gamma E m \sec(x) - E^2 - m^2 \gamma^2 - m^2 \tan^2(x) \\ = (E^2-m^2) \gamma^2 \beta^2 - (\gamma E - m \sec(x))^2 = H^2 - K^2$

Use

$\alpha \gamma \beta z \rightarrow Z \\ \beta \gamma \alpha a \rightarrow G$

We have,

$\displaystyle Z = K \left( 1 - \frac{G}{\sqrt{H^2 - K^2}} \right)$

Next, change or replace,

$\displaystyle K \rightarrow H \sin(\phi), -\frac{\pi}{2} < \phi < \frac{\pi}{2}$

$\displaystyle Z = H \sin(\phi) - G \tan(\phi)$

Since $H , G > 0$ , and $G < H$ , as

$\displaystyle \frac{G}{\sqrt{H^2 - K^2 }} = \frac{a}{2\pi\rho} < 1$

The function

$f(\phi) = H \sin(\phi) - G \tan(\phi)$

looks like the orange line below

The blue line is $f(\phi) = Z$ . It seems that there are multi-solution for $\phi$ . When $\theta_{cm} >> 0$ ,

$f'(\phi) = H \cos(\phi) - G \sec^2(\phi) > 0$

Thus, there is only one solution. However, when $\theta_{cm}$ is small, there is multi-solution. That need to be careful.

HELIOS constant thetaCM line

October 30, 2018

GoLuckyRyan Basic HELIOS, transfer reaction Leave a comment

somehow I confused the term “line”, because sometimes it means a “curve”, anyway~

There is a plot of the energy – z-pos plot (EZ-plot) in the last post. In the EZ plot, the constant excitation energy line is already given in the equation (3) in this post. And the finite-detector correction is presented in the last post. The constant $\theta_{CM}$ line is

$\displaystyle E = \frac{-\sin^2(\theta_{CM}) \alpha \beta \gamma^2 z + \cos(\theta_{CM})\sqrt{\alpha^2 z^2 + m_b^2 (1-\sin^2(\theta_{CM})\gamma^2)}}{1-\sin^2(\theta_{CM})\gamma^2}$

where $\alpha = \frac{cZB}{2\pi}$

you can guess/see that, this is a solution of a quadratic equation. In fact, from the equation (1) and (2) in this post, by eliminating the $\cos(\theta_{CM})$ in $\vec{\beta} \cdot \vec{p}$ , we got the constant $E_x$ line. By eliminating the $m_B$ (the mass of the heavier particle, or the excited energy) in $E_{cm}$ (see $E_{tot}$ in this post ), we got the above equation.

When $\theta_{CM} = 0$ , the equation reduces to

$\displaystyle E = \sqrt{\alpha^2 z^2 + m_b^2}$

OK, I know I skipped a lot of step, which is not my style. From the equation (1) and (2), eliminate $E_{cm}$ gives you,

$\displaystyle E = \frac{\alpha}{\beta}z - \frac{1}{\gamma}(\vec{\beta}\cdot\vec{p})$

it is a linear! But if you look closely, the center of mass momentum has explicit $E_x$ dependence, it is a constant of motion only when $E_x$ is constant. The higher the excitation energy, the less energy of the recoil energy $E$ of the proton! Thus, it is like $p = p(E_x) = p(E_x(E))$ . A more easy way to eliminate $m_B$ or $E_x$ , is expand $E_{cm}$ into

$\displaystyle E_{cm} = \frac{1}{E_{tot}}\left( E_{tot}^2 + m_b^2 - m_B^2\right)$

Thus, eliminating $m_B = (m_B)_{g.s.} + E_x$ by isolate $m_B$ .

Finite detector effect in HELIOS

October 26, 2018

GoLuckyRyan Basic HELIOS, transfer reaction Leave a comment

I was very busy last month that I went to CERN to join two experiments. The experiments were using ISOLDE Solenoid Spectrometer, which is a HELIOS-type equipment. In fact, I planned to post a series about HELIOS spectrometer, mainly focus on the kinematics, to address different detail, like offset-beam effect, tilted-beam effect, the constant-thetaCM line, etc., but I was very busy, probably until Dec. Anyway~

The pervious post lay the foundation for HELIOS spectrometer. The energy and z-position is linear, that simplified a lot of things. And the Q-value or excitation energy is in the intercept and in most cases, can be linearly approximated, i.e. $E_x \propto E_{cm}$ . We can derive the exact relation later.

Screen Shot 2018-10-26 at 23.41.44.png

In the above plot, 28Mg(d,p) at 9.43 MeV/u. The dashed line is for infinite detector, the red line is for finite detector, and the blue line is 0 deg center of mass angle. We can see, for smaller energy, the change of the hit-position is larger and non-linear. It is because at smaller energy, the scattered angle is small, and the particle hits the detector at very small angle ( with respect to the detector plane, not detector normal), so that the particle will be stopped much earlier.

Today, I will show the algebraic solution for finite detector effect.

Finite detector effect, from it name, because the detector has size, so the hit position is difference from the on-axis position. Below is the x-y plane view, the detector plane is the orange line, with distance from the z-axis of a and make an angle $\phi_p$ to the x-z plane. The blue line is the helix curve of the charged particle in the magnetic field. The radius of the helix curve is $\rho$ , and the emittance angle of the particle is $\phi$ .

Screen Shot 2018-10-26 at 23.07.48.png

If the particle hit back the z-axis, the $\Delta \phi = 2\pi$ , but due to finite detector size, it will not complete a cycle.

The equation of the detector plane is

$\displaystyle x\cos(\phi_p)+ y\sin(\phi_p) = a$

The equation of the locus of the particle is

$\displaystyle \begin{pmatrix} x \\ y \end{pmatrix} = \rho \begin{pmatrix} \sin(\tan(\theta) \frac{z}{\rho} - \sin(\phi)) \\ \cos(\phi) - \cos(\tan(\theta) \frac{z}{\rho} \end{pmatrix}$

where, $\theta$ is the particle emittance with respect to the z-axis. Solving these two equation for $z$ , we have

$\displaystyle z = \frac{\rho}{\tan(\theta)}\left( \phi_p - \phi + n\pi + (-1)^{n} \sin^{-1}\left( \frac{a}{\rho} + \sin(\phi-\phi_p) \right) \right), n=0,1,2,...$

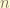where $n$ is the number of time that the particle crossed the detector plan. Note that, the length of a cycle is

$\displaystyle z_0 = 2\pi \frac{\rho}{\tan(\theta)}$

In the case when $\phi = 0$ , $\phi_p = \pi$ , and we want the particle hit from the outside, i.e. $n = 2m+1, m = 0, 1,2,..$ , the solution becomes

$\displaystyle z = z_0 \left( 1 - \frac{1}{2\pi}\sin^{-1}\left( \frac{a}{\rho} \right) \right)$

When $\rho >> a$ ,

$\displaystyle z \approx z_0 \left( 1 - \frac{1}{2\pi} \frac{a}{\rho}\right)$

In transfer reaction, when the beam energy is fixed, the degree of freedom is 2: the excitation energy ( $E_x$ ) and center of mass angle ( $\theta_{cm}$ . After the HELIOS, the observables are energy ( $e$ ) and z-position ( $z$ ). With the finite detector effect, the mapping look like this

Screen Shot 2018-10-26 at 23.52.27.png

We can see, there are some regions that the manifold of $E_x - \theta_{cm}$ is folded. So, there is no way to have an inverse transform to get back the $E_x$ and $latex_{cm}$ from the observables. Unless, we can, somehow, extrapolating the z-axis position.

Kinematics in Magnetic field

September 18, 2018

GoLuckyRyan Basic 2-body reaction, HELIOS, transfer reaction Leave a comment

Generally, the best starting point of any kinematics calculation for any reaction is from the CM frame. In the exit channel, the four-momentum in the CM frame is

$P_{cm} = \begin{pmatrix} \sqrt{m^2 + p^2} = E_{cm} \\ \vec{p} \end{pmatrix}$

the boost from CM frame to Lab frame is $\vec{\beta}$ . Lets define the perpendicular vector on the plane of $\vec{p}$ be $\hat{n}$ , thus, the four-momentum in the Lab frame is

$P = \begin{pmatrix} E \\ \vec{k} \end{pmatrix} =\begin{pmatrix} \gamma E_{cm} + \gamma \beta \hat{\beta}\cdot \vec{p} \\ \left( \gamma \beta E_{cm} + \gamma (\hat{\beta} \cdot \vec{p}) \right) \hat{\beta} + (\hat{n} \cdot \vec{p} ) \hat{n} \end{pmatrix}$

where

$\displaystyle E_{cm} = \frac{1}{2E_t}\left( E_t^2 + m_b^2 -m_B^2 \right)$

$\displaystyle p^2 = \frac{1}{4E_t^2} \left(E_t^2 - (m_b + m_B)^2\right) \left(E_t^2 - (m_b - m_B)^2\right)$

$\displaystyle E_t^2 = (m_a+m_A)^2 + 2m_aT$

$\displaystyle \beta = \frac{\sqrt{(m_A+T)^2 - m_A^2}}{m_a + m_A + T}, \gamma = \frac{1}{\sqrt{1-\beta^2}}$

We can see, the particle-A is moving with kinematic energy of $T$ , hit particle-a, result in particle-b and particle-B.

Suppose the magnetic field is parallel to z-axis

$\vec{B} = B \hat{z}$

The rotation radius is

$\displaystyle \rho = \frac{\vec{k} \cdot \hat{xy} }{cZB}$

where $Z$ is the charge state of the particle, and $\hat{xy}$ is the perpendicular unit vector on xy-plane.

The time for 1 cycle is

$\displaystyle T_{cyc} = \frac{2\pi \rho}{v_{xy}} = \frac{2\pi}{cZB} \frac{\vec{k}\cdot\hat{xy}}{v_{xy}} = \frac{2\pi}{c ZB} \frac{E}{c}, ~~ E \frac{v}{c} = |\vec{k}|$

And the length for 1 cycle is

$\displaystyle z_{cyc} = v_z T_{cyc} = \frac{2\pi}{cZB} \vec{k}\cdot \hat{xy} \frac{v_z}{v_{xy}} = \frac{2\pi}{cZB} \vec{k}\cdot \hat{z}$

When the Lorentz boost is parallel to the B-field direction,

$\vec{\beta} \cdot \hat{z} = 1, \hat{n} \cdot \hat{z} = 0$

$\displaystyle z_{cyc} = \frac{2\pi}{cZB} \left(\gamma \beta E_{cm} + \gamma (\hat{\beta} \cdot \vec{p})\right)$ ………………. (1)

and the total energy is

$\displaystyle E = \gamma E_{cm} + \gamma \beta (\hat{\beta}\cdot \vec{p})$ …………….. (2)

By eliminating the $\hat{\beta} \cdot \vec{p}$ ,

$\displaystyle E = \frac{1}{\gamma}E_{cm} + \frac{cZB}{2\pi} \beta z_{cyc}$ …………….. (3)

We can see that, the energy and $z_{cyc}$ have a linear relation. That simplified a alot of thing. For instance, the intercept is related to $E_{cm}$ , which is further related to the Q-value of the reaction. If we can plot the E-z plot and determine the intercept, we can extract the Q-value, which is related to the excitation energy or some sort.

Without the magnetic field, to extract the Q-value, we really need to know the scattering angle (the azimuthal angle can be skipped due to symmetry in some cases). And usually, the relation is not linear.

Momentum Matching in Transfer Reaction

January 29, 2018

GoLuckyRyan Basic, Scattering, theory transfer reaction Leave a comment

In transfer reaction, the kinematics determines the scattering angles and momenta, but it does not tell the probability of the reaction. Not all angle have same cross section, because when a particle is being transfer to or pickup from a nucleus, the momentum has to be matched. It is like a spaceship need a proper angle and speed in order to orbit around the earth, it the incident angle or speed are not good, the spaceship will just go out or crash into the earth.

Suppose our reaction is $A(B,1)2$ , $A$ is incident particle, $B$ is the target, $1, 2$ are the outgoing particles. The momentum transfer from $A$ via $2$ to $B$ or $1$ is

$\vec{q} = \vec{p}_2 - \vec{p}_A = \vec{p}_f - \vec{p}_i$

where $\vec{p}_i$ is initial momentum and $\vec{p}_f$ is final momentum.

Assume the reaction take place at the surface of nucleus $B$ . The maximum angular momentum it can create is

$\vec{L} = \vec{r} \times \vec{q} \rightarrow L = r q$

In QM, the angular momentum must be $L = \sqrt{l(l+1)} \hbar$ . Here we pause for unit conversion. In this blog, we usually using nuclear unit, that momentum in [MeV/c] and $\hbar = 197.327 \textrm{MeV fm/c}$ , thus, to calculate the angular momentum, simple multiple the momentum in MeV/c and nuclear radius in fm. The radius of a nucleus is roughly $r = 1.25 A^{1/3} \textrm{fm}$ .

So, if the momentum $\sqrt{(l+1)(l+2)} \hbar > r|q| > \sqrt{l(l+1)} \hbar$ , the possible angular momentum is $\sqrt{l(l+1)} \hbar$ or the l-orbit.

In the transfer reaction, the equation for $\vec{p}_k$ and $\vec{p}_i$ are known. It is straight forward to calculate $r q / \hbar$ , plot against scattering angle, and we look for the value for $\sqrt{l(l+1)}$ .

Or, we can scale the y-axis by

$\displaystyle y' = \sqrt{\left(q\frac{r}{\hbar}\right)^2 + \frac{1}{4}} - \frac{1}{2}$

The new y-axis is in unit of $\sqrt{l(l+1)}$ .

We can also plot the contour of momentum matching on the $p_k$ versus scatering angle. The momentum matching is

$\displaystyle q^2 = \frac{l(l+1)\hbar^2}{r^2} = p_f^2 + p_i^2 - 2 p_f p_i \cos(\theta)$

where $\theta$ is the scattering angle of particle $1$ . Solve for $p_f$

$\displaystyle p_f = p_i \cos(\theta) \pm \sqrt{ \left( \frac{l(l+1) \hbar^2}{r^2} \right) - k_i^2 \sin^2(\theta) }$

We can plot the contour plot for difference $l$ . and then overlap with the momentum and the scattering angle of the outgoing particle $2$ .

Screen Shot 2018-01-30 at 14.31.12.png

a correction, the y-axis should be $p_2$ , momentum of particle 2.

Kinematics of Transfer Reaction

January 17, 2018

GoLuckyRyan Basic, Scattering kinematics, transfer reaction Leave a comment

Another surprise that no post on the kinematics of transfer reaction!

Suppose the reaction is $A(B, 1)2$ , where $A$ is the incident particle, $B$ is the target nucleus that is at rest, $1, 2$ are the outgoing particle.

The Q-value for the reaction is the difference between initial mass and final mass

$Q = m_A+ m_B - m_1-m_2$

When the incident energy is too low, lower then the Q-value (we will see the relationship later) , the reaction is impossible, because the nuclei-1 and 2 cannot be created.

The equation for the reaction is

$P_A + P_B = P_1 + P_2$

where $P_i$ are 4-momenta. The number of freedom is 2. The total unknown is 8 from $P_1, P_2$ , the masses of particle-1, and -2 give 2 constrains, the equations give 4 constrains.

$P_A = ( E_A , 0, 0, k_A) = ( m_A + T_A, 0, 0, \sqrt{2 m_A T_A + T_A^2})\\ P_B = (m_B, 0, 0, 0)$

where $T_A$ is the incident energy. We first transform the system into center of momentum (CM) frame. Since the total momentum is zero in the CM frame, we construct a CM 4-momentum

$P_{cm} = (P_A+P_B)/2 = ( m_A+ m_B + T_A, 0, 0, k_A)$

The Lorentz beta is $\beta = k_A/(m_A+m_B+T_A)$ .

The invariance mass of the CM 4-momentum is unchanged, which is equal to the total energy of the particles in the CM frame. We can check

$P_A' = ( \gamma E_A - \gamma \beta k_A, 0, 0, -\gamma \beta E_A + \gamma k_A) \\ P_B' = ( \gamma m_B , 0, 0, -\gamma \beta m_B )$

The total energy in CM frame is

$E_{tot} = \gamma( m_A+m_B + T_A) - \gamma \beta k_A = \sqrt{(m_A+m_B+T_A)^2 - k_A^2}$

After the reaction, the momenta of the particle-1 and -2 are the same an opposite direction in the CM frame.Balancing the energy and momentum, the momentum is

$\displaystyle k = \frac{1}{2 E_{tot}} \sqrt{(E_{tot}^2 - (m_1+m_2)^2)(E_{tot}^2 - (m_1-m_2)^2)}$

In the equation, if either of the bracket is negative, the momentum cannot be formed. The smaller term is

$E_{tot}^2 - (m_1+m_2)^2 = (m_A+m_B+T_A)^2 - k_A^2 - (m_1+m_2)^2 \\ =(m_A+m_B+T_A)^2 - k_A^2 - (m_A+m_B-Q)^2 \\ = 2m_BT_A + 2(m_A + m_B)Q - Q^2$

If we set the line for this quantity be zero,

$\displaystyle 2m_BT_A + 2(m_A + m_B)Q - Q^2 = 0 \\ T_A = \frac{Q^2 - 2(m_A+m_B)}{2m_B} \\ = \frac{1}{2m_B} ( (Q-m_A-m_B)^2 - (m_A+m_B)^2) \\ = \frac{1}{2m_B} ( (m_1+m_2)^2 - (m_A+m_B)^2)$

Thus, if the $T_A$ is smaller then that value, the reaction is impossible.

The 4-momenta of the outgoing particles can be constructed.

$P_1' = ( \sqrt{m_1^2 - k^2} , k \cos(\phi) \sin(\theta) , k \sin(\phi) \sin(\theta) , k \cos(\theta)) \\ P_2' = ( \sqrt{m_2^2 - k^2} , -k \cos(\phi) \sin(\theta) ,- k \sin(\phi) \sin(\theta) , -k \cos(\theta))$

Back to Lab frame,

$P_1 = \begin{pmatrix} \gamma \sqrt{m_1^2 + k^2} + \gamma \beta k \cos(\theta) \\ k \cos(\phi) \sin(\theta) \\ k \sin(\phi) \sin(\theta) \\ \gamma \beta \sqrt{m_1^2 - k^2} + \gamma k \cos(\theta)\end{pmatrix}$

For simplicity, set $\phi = 0$ ,

$P_1 = \begin{pmatrix} \gamma \sqrt{m_1^2 + k^2} + \gamma \beta k \cos(\theta) \\ k \cos(\phi) \sin(\theta) \\ 0 \\ \gamma \beta \sqrt{m_1^2 - k^2} + \gamma k \cos(\theta) \end{pmatrix}$

We can see, the locus in the momentum space is

$( k cos(\phi) \sin(\theta) , 0, \gamma \beta \sqrt{m_1^2 - k^2} + \gamma k \cos(\theta))$

This is an ellipse with length $k (1, \gamma)$ , and centered at $(0, \gamma \beta \sqrt{m_1^2 + k^2})$ . If the relativistic effect is small, it is a circle.

When the ellipse long axis $\gamma k$ is longer then the center position $\gamma \beta \sqrt{m_1^2 + k^2}$ , the scattering angle can be to whole circle, i.e.

$\displaystyle \gamma \beta \sqrt{m_1^2 + k^2} < \gamma k \rightarrow \gamma \beta m_1 < k$

in here, we can treat $\gamma \beta m_1 = k_\beta(1)$ , this is the momentum “gain” from shifting from CM frame to Lab frame. By compare $k_\beta(1)$ or $k_beta(2)$ to $k$ we can know the span of scattering angle.

Here is an example,

Screen Shot 2018-01-30 at 14.54.31.png

Nuclear Physics 101

PRL paper

HELIOS – an inverse problem

HELIOS constant thetaCM line

Finite detector effect in HELIOS

Kinematics in Magnetic field

Momentum Matching in Transfer Reaction

Kinematics of Transfer Reaction

Recent Posts

Calendar

Archives

Keywords

# of Visitors

Login