Simple RC circuit

January 19, 2022

GoLuckyRyan Basic Leave a comment

The voltage across a resistor with current I is

\displaystyle V_R = I R

The voltage across a capacitor with charge Q is

\displaystyle V = Q/C

The equation for a RC circuit is

\displaystyle V = IR + \frac{Q}{C}

If we want to find the voltage across the capacitor, the direct way is solving Q.

\displaystyle V = R \frac{dQ}{dt} + \frac{Q}{C}

For a DC voltage switched on at t = 0, the solution of Q of

\displaystyle \frac{dQ}{dt} = \frac{V_0}{R} - \frac{1}{RC} Q

takes the form Q(t) = A\exp(a t) + B, and with initial condition Q(0) = 0, plug in

\displaystyle A a \exp(at) = \frac{V_0}{R} - \frac{1}{RC} (A \exp(a t) + B )

Thus, we get B = V_0 C, A = - B, a = -\frac{1}{RC} . Thus, the solution is

\displaystyle Q(t) = V_0 C \left( 1- \exp\left(-\frac{t}{RC} \right) \right)

We can differentiate and get the current

\displaystyle I(t) = \frac{V_0}{R} \exp\left( - \frac{t}{RC}\right)

In the AC case, it is easy to do it using complex number. Let the voltage be V(t) = V_0 \exp(i \omega t ), and we solve

\displaystyle V_0 e^{i\omega t} = R \frac{dQ}{dt} + \frac{Q}{C}

The solution must be have the form that driving from the source e^{i\omega t} and also the e^{-t/RC}, from the intrinsic motion of the RC circuit.

\displaystyle Q(t) = A e^{i\omega t} + B e^{-t/RC}

another way to guess this form is that, the 1st term is also driving by the source, the 2nd term is the homogeneous solution that source term is zero.

with initial condition Q(0) = 0, we have A = -B

plug in to the equation, and we get,

\displaystyle V_0 C e^{i\omega t} = R C \left(A i \omega e^{i\omega t} + \frac{A}{RC} e^{-t/RC} \right) + A e^{i\omega t} -A \exp{-t/RC}

compare e^{i\omega t} , we have

\displaystyle V_0 C = RCA i \omega + A \rightarrow A = \frac{V_0 C}{ 1 + i \omega RC}

compare e^{-t/RC} , we have

\displaystyle 0 = A - A

Thus, we have the solution

\displaystyle Q(t) = \frac{V_0 C}{1 + i \omega RC} \left( e^{i \omega t} - e^{-t/RC} \right)

And the current is

\displaystyle I(t) = \frac{V_0 C}{1 + i \omega RC} \left( i \omega e^{i \omega t} + \frac{1}{RC} e^{-t/RC} \right)

The last step converts back to real value.

\displaystyle Q(t) = \frac{V_0 C}{1 + \omega^2 R^2C^2} (1 - i \omega RC)\left( \cos(\omega t) + i \sin(\omega t) - e^{-t/RC} \right) \\ = \frac{V_0 C}{1 + \omega^2 R^2C^2}( \cos(\omega t) + \omega RC \sin(\omega t) - e^{-t/RC} \\ ~~~~~~~~~ - i \omega RC \cos(\omega t) + i \sin(\omega t) +i \omega RC e^{-t/RC} )

Thus, If the input is V(t) = V_0 \cos(\omega t) , The charge is

\displaystyle Q(t) = \frac{V_0 C}{1 + \omega^2 R^2C^2} \left( \cos(\omega t) + \omega RC \sin(\omega t) - e^{-t/RC} \right)

else, if the input is V(t)= V_0 \sin(\omega t), the charge is

\displaystyle Q(t) = \frac{V_0 C}{1 + \omega^2 R^2C^2} \left( -\omega RC \cos(\omega t) + \sin(\omega t) + \omega RC e^{-t/RC} \right)

We can see that, the size of the voltage across the capacitor is

\displaystyle V_C(t) = \frac{V_0}{1 + \omega^2 R^2C^2} \left( \cos(\omega t) + \omega RC \sin(\omega t) - e^{-t/RC} \right)

when \omega = 1/RC , the voltage is only half of the source voltage, and higher the frequency, lower of the voltage. Thus, it is called low-pass filter for this characteristics.

In long term, the e^{-t/RC} term will go away, the stable current is

\displaystyle I(t) = \frac{V_0 i \omega C}{1 + i \omega RC} e^{i \omega t} = \frac{i\omega C}{1 + i \omega RC} V(t)

In fact, we can use impedance to get this result. ( or impedance was discovered from this result ).

The impedances Z for a resistor is R, for a capacitor is 1/(i\omega RC) , and for a inductor is i\omega L.

For an RC circuit, the equation is

\displaystyle V = I ( Z_R + Z_C ) = I \left( R + \frac{1}{i\omega C} \right)

solve for the current, we have

\displaystyle I(t) = \frac{i\omega C}{1+ i\omega RC} V(t) .

And we can write

\displaystyle \frac{i\omega C}{1+ i\omega RC} = \frac{\omega C}{\sqrt{1 + \omega^2 R^2C^2}} e^{i\theta}, \theta = \tan^{-1}\left( \frac{1}{\omega RC} \right)

And the current is

\displaystyle I(t) = \frac{\omega C}{\sqrt{1+ \omega^2 R^2C^2}} V_0 e^{i \omega t + i \theta } .

This shows that in AC circuit, there is a phase different between input voltage and current.

Smith Chart ( quick guide )

June 1, 2011

GoLuckyRyan circuits, theory Leave a comment

for the coaxial cable is ¼ wavelength, everything in transmission line theory will be simplified.

the input impedance will be

Z_{in} = Z_0 \frac{1-\Gamma}{1+\Gamma}

where Γ is the characteristic impedance:

\Gamma = \frac{ Z_L - Z_0 }{Z_L + Z_0}

and the reflection wave and input wave ratio is :

\rho = \left| \frac{V_-}{V_+} \right| = |\Gamma|

these are 3 important equations on smith chart.

we can use normalized impedance, which is defined as

z_{in} = Z_{in}/Z_0

z_L = Z_L / Z_0

than  2 of the  3 equations will be normalized to :

z_{in}= \frac{1-\Gamma}{1+\Gamma}

$latex \Gamma = \frac{ z_L – 1 }{z_L + 1} $

by setting z_{in} = r + i x , we have :

\Gamma = \frac{ 1- r^2 - x^2 }{(1+r)^2+x^2} - i \frac{2x}{(1+r)^2+x^2}

by some algebra, we have :

z_{in} = 1/ z_L

which is the result for ¼ wavelength cable. by this,we have:

z_L = \frac{r}{r^2+x^2}- i \frac{x}{r^2+x^2}

after many equations, for impedance matching, we have following equivalent statements.

  • impedance matching
  • z_L = 1
  • \Gamma = 0
  • z_{in} = 1
  • \rho = 0 , no reflected wave

OK. the math is over. The Smith Chart is the Cartesian coordinate for Γ, real axis on horizontal, imagine axis on vertical. and the circles, are the transformed coordinate of the input impedance. the transformation is called Möbiüs  transform.

a good impedance matching can be found at the origin of the chart, where \Gamma = 0 + 0 i , and if we read the input impedance coordinate, it is z_{in} = 1 + 0 i , which mean, impedance matched.

However, there is never so ideal in real world. the input impedance always has some imaginary part, or real part not equal to 1. so, what if, both of them are different by 0.2 or 10 Ohm?

 

[Pol. p target] Matching Impedance of NMR coil

March 8, 2011

GoLuckyRyan Lab Log , , 5 Comments

i had played with the impedance of coax cable. connect the signal generator at 50Ω output and a 4meter long coax to a CRO with 50Ω input with a tee. although the web said, the coax impedance is 52, there is no observed different. the peak-to peak signal does not depend on the frequency.

then connect a 12.8MHz coax to the tee and open at the other end. in theory, it should be zero input-impedance and he CRO reading should be

V_{in}= 1 - cos( 2\pi L/\lambda)

where the CRO reading is the input voltage. when the frequency adjusted to 12.8MHz, which is quata-wavelength, the input voltage is equal to 1.

when connect the end of the coax with a 50Ω resistor, the input voltage does not depends on frequency, as expected.

i haven’t try to short the end of the coax.

after that. i going to matching the impedance of the tuner and coil. we use a short coax to connect the input to the tuner before, i replaced it with a 12.8MHz coax. the reason is, the little bit mismatching of the impedance can be saved by the length of the cable, such that:

Z_{in} = Z_0^2/Z_L \approx Z_0

and i opened the tuner to see the circuit inside:

The above is the circuit diagram. there is a fixed capacitor with 2.2pF in parallel. i cannot identify the type of the 2 variable capacitor.  the coax cable can be put in port 1 or port 2 and the coil put in the other port. different configuration has different behavior.

i found that, the input is in port 2 and the coil is in port 1, and the box doesn’t ground but just wrapped with metal sticker. i took it out and grounded to NMR system.

For the input at port 2, the total impedance of the coil and tuner is:

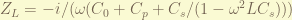
Z_L= - i /(\omega (C_0+C_p + C_s/(1-\omega^2 L C_s)))

The first things to notice is the impedance depends on the frequency. which mean, the impedance matching can only on particular frequency. when the Cs adjusted to matching the frequency. the impedance solely depends on Cp. when the driving voltage gone, the LC circuit will oscillate at natural frequency:

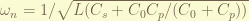
\omega_n = 1/\sqrt{ L ( C_s + C_0 C_p / (C_0+C_p) ) }

Thus, i tired to measure to inductance of the coil by a parallel resistance. but i cannot find any suitable wire to convert BNC cable to wires. after a long time finding, i gave up and wait unit work with my partner.

the input in port 2 is not a common config, so, i changed it to port 1. and the impedance is :

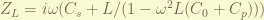
Z_L=i\omega (C_s +L/(1-\omega^2L(C_0+ C_p)))

The impedance also depends on frequency. and the natural frequency when the driving voltage gone is:

\omega_n = 1/\sqrt{L(C_0+C_p)}

there is one way to tune the Cp to match the input frequency and make load impedance solely depends on Cs. by using a pulse signal. and measure the natural frequency of the LC loop, such that the natural frequency is same as input frequency. However, the Low Pass Filter only let frequency less then 1MHz pass and out frequency is 12.8MHz. can i use other pulse source? may be, if i have a mixer.

so, i matching the impedance by very naive way. i use the method on testing the impedance matching. i use a continuous signal source and fixed the frequency at 12.8MHz, then connect it with a coax cable to 50Ω CRO input by a tee, then connect th tee with a 12.8MHz coax cable. the other end of the cable connect to a 50Ω resistor. this setup should be matched impedance. so, i record the input voltage on the CRO. and replace the resistor with the tuner, which port 2 connected to the coil. then adjust the capacitors (both) so that the CRO voltage is same as 50Ω resistor.

by solving the load impedance formula of port 1 configuration, there are mulitple solution for Cp and Cs to give 50Ω. and i think, as long as the impedance is 50Ω at 12.8MHz, any configuration can do the job.

later, i try to find the water NMR signal. although i cannot find any. but the noise level reduced to ±5mV. more or less equal to the background.

i played with the NMR program. the record data is counted by point, so the CRO horizontal setting should set to 5000 points over the screen.

and just before i leave, i don’t know what wrong, the program doesn’t read the CRO signal…

Transmission Line

February 12, 2011

GoLuckyRyan Basic, circuits, others , , , , , 1 Comment

a Transmission Line is any thing used to transmit a electric signal.

in a AC circuit, the voltage does not only variate on time but also on space. For low frequency, the wavelength is long and this can be neglected. But at hight frequency, the variation is significant.

since the voltage is changing from different location. we cut the transmission line in a small sector, and each sector is analog to some circuit elements, no matter the shape of the line. this gives us a easy understanding of what is going on for the voltage and current. But this analogy neglected the effect of temperature, material non-linearity and magnetic hysteresis effect.

the equation of voltage across a section is

V(x) = ( R + i \omega L )\Delta x I(x)+ V(x+\Delta x )

since the resistance and inductance have unit per length. rearrange and take limit of x.

- \frac {d V(x)}{dx} = ( R + i \omega L ) I(x)

the equation of current is

I(x) = ( Q + i \omega C )\Delta x V(x+ \Delta x) + I(x+ \Delta x )

The Q is conductance, which is NOT an invert of resistance in case of AC. both Q and C will draw some current away in AC circuit. take limit gives

- \frac { d I(x) }{dx} = (Q + i \omega C ) V(x)

now we have 2 coupled equations. If we de-couple them, we will have

\frac {d^2 V(x)}{dx^2} = k^2 V(x)

k = \sqrt{ (R+i \omega L ) ( Q + i \omega C ) }

and the current share the same equation. notice that k is a complex number.

the solution are:

V(x) = V_f Exp( - k x ) + V_b Exp( k x)

I(x) = I_f Exp( - k x) + I_b Exp( k x )

where the subscript means forward and backward. from the coupled equation of Current, we can related the voltage and current and find out the impedance.

V(x) = \sqrt{ \frac { R+ i \omega L } { Q + i \omega C } } (I_f Exp(-kx) - I_b Exp(k x)

Thus, we define the Characteristic Impedance for forward wave.

Z_0 = \sqrt{ \frac { R+ i \omega L } { Q + i \omega C }}

the Characteristic Impedance for backward wave is a minus sign. there fore, we can rewrite the current in term of voltage.

I(x) = \frac {1}{Z_0} ( V_f Exp(-kx) - V_b Exp(kx)

_________________________________________

impedance matching

for a load at the end of the transmission line, the wave will get reflected. to see this, we have to consider the load, which imposed another equation. the voltage across the load is:

V(L) = V_f Exp( - k L ) + V_b Exp( k L)

and the current input to the load is:

I(L) = \frac {1}{Z_0} ( V_f Exp(-kL) - V_b Exp(kL)

the current and the voltage is related by:

V(L) = Z_L I(L)

solve it, and find the ratio of :

\frac { V_b }{V_f} = Exp( - 2 k L ) \frac { Z_L - Z_0 }{ Z_L + Z_0 }

since we can do nothing on the exponential, thus, we define a reflection coefficient:

\Gamma_0 = \frac { Z_L - Z_0} {Z_L - Z_0}

for no reflected wave, the impedance of the load and the transmission line should be equal and it is called impedance matching.

the power of the load is:

P = V(L)I*(L) = \frac { 1}{Z_0} ( V_f^2 Exp( - 2 k L ) - V_b^2 Exp( 2k L) + V_f V_b* -V_f* V_b )

when the impedance is matched, the power is maximum.

 

 

I-V Converter

February 11, 2011

GoLuckyRyan Basic, circuits, experimental, Lab Log, no math, others , Leave a comment

It is a current to voltage converter. the ratio of the converted voltage to the input current is notated as the K-factor, which indicated that the converter may amplify the signal as well.

The reason for study a I-V converter is due to the experiment’s needs, that we have a current output but we want to know the size of the current without affecting the circuit.

A simple I-V converter is made by 1 single resistance. When a current passes the resistance, a voltage is built across it. If we measure the voltage with an infinite load voltage meter, then no current will go to the voltmeter and system is unaffected. In this case, the resistance of the resister is the K-factor.

However, we normally deal with an AC signal, which is oscillating with frequency.

If the converter amplify the AC signal, it has capacitance and reactance (impedance) depends on input frequency.  So, we have to choose a correct range of working frequency of the converter.