The rotation of a vector in a vector space can be done by either rotating the basis vector or the coordinate of the vector. Here, we always use fixed basis for rotation.
For a rigid body, its rotation can be accomplished using Euler rotation, or rotation around an axis.
Whenever a transform preserves the norm of the vector, it is a unitary transform. Rotation preserves the norm and it is a unitary transform, can it can be represented by a unitary matrix. As a unitary matrix, the eigen states are an convenient basis for the vector space.
We will start from 2-D space. Within the 2-D space, we discuss about rotation started by vector and then function. The vector function does not explicitly discussed, but it was touched when discussing on functions. In the course, the eigen state is a key concept, as it is a convenient basis. We skipped the discussion for 3-D space, the connection between 2-D and 3-D space was already discussed in previous post. At the end, we take about direct product space.
In 2-D space. A 2-D vector is rotated by a transform R, and the representation matrix of R has eigen value

and eigenvector

If all vector expand as a linear combination of the eigen vector, then the rotation can be done by simply multiplying the eigen value.
Now, for a 2-D function, the rotation is done by changing of coordinate. However, The functional space is also a vector space, such that
 still in the space,
still in the space,- exist of unit and inverse of addition,
- the norm can be defined on a suitable domain by

For example, the two functions  , the rotation can be done by a rotational matrix,
, the rotation can be done by a rotational matrix,

And, the product  also from a basis. And the rotation on this new basis was induced from the original rotation.
also from a basis. And the rotation on this new basis was induced from the original rotation.

where  . The space becomes “3-dimensional” because
. The space becomes “3-dimensional” because  , otherwise, it will becomes “4-dimensional”.
, otherwise, it will becomes “4-dimensional”.
The 2-D function can also be expressed in polar coordinate,  , and further decomposed into
, and further decomposed into  .
.
How can we find the eigen function for the angular part?
One way is using an operator that commutes with rotation, so that the eigen function of the operator is also the eigen function of the rotation. an example is the Laplacian.
The eigen function for the 2-D Lapacian is the Fourier series.
Therefore, if we can express the function into a polynomial of  , the rotation of the function is simply multiplied by the rotation matrix.
, the rotation of the function is simply multiplied by the rotation matrix.
The eigen function is

The D-matrix of rotation (D for Darstellung, representation in German)  is
is

The delta function of  indicates that a rotation does not mix the spaces. The transformation of the eigen function is
indicates that a rotation does not mix the spaces. The transformation of the eigen function is

for example,

write in polar coordinate

where  .
.
The rotation is

If we write the rotated function in Cartesian form,

where  .
.
In 3-D space, the same logic still applicable.
The spherical harmonics  serves as the basis for eigenvalue of
serves as the basis for eigenvalue of  , eigen spaces for difference
, eigen spaces for difference  are orthogonal. This is an extension of the 2-D eigen function
are orthogonal. This is an extension of the 2-D eigen function  .
.
A 3-D function can be expressed in spherical harmonics, and the rotation is simple multiplied with the Wigner D-matrix.
On above, we show an example of higher order rotation induced by product space. I called it the induced space (I am not sure it is the correct name or not), because the space is the same, but the order is higher.
For two particles system, the direct product space is formed by the product of the basis from two distinct space (could be identical space).

Some common direct product spaces are
- combining two spins
- combining two orbital angular momentum
- two particles system
No matter induced space or direct product space, there structure are very similar. In 3-D rotation, the two spaces and the direct product space is related by the Clebsch-Gordon coefficient. While in 2-D rotation, we can see from the above discussion, the coefficient is simply 1.
Lets use 2-D space to show the “induced product” space. For order  , which is the primary base that contains only
, which is the primary base that contains only  .
.
For  , the space has
, the space has  , but the linear combination
, but the linear combination  is unchanged after rotation. Thus, the size of the space reduced
is unchanged after rotation. Thus, the size of the space reduced  .
.
For  , the space has
, the space has  , this time, the linear combinations
, this time, the linear combinations  behave like
behave like  and
and  behave like
behave like  , thus the size of the space reduce to
, thus the size of the space reduce to  .
.
For higher order, the total combination of  is
is  , and we can find
, and we can find  repeated combinations, thus the size of the irreducible space of order
repeated combinations, thus the size of the irreducible space of order 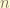 is always 2.
is always 2.
For 3-D space, the size of combination of  is
is  . We can find
. We can find  repeated combination, thus, the size of the irreducible space of order
repeated combination, thus, the size of the irreducible space of order 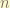 is always
is always  .
.
, the Clebsh-Gordon coefficient dictated that
,
,
.
fm. the wave function is spherical Bessel function ,
,
is the normalization factor.

-th s-state is

.






