spin | Nuclear Physics 101

Magnetic Dipole Moment & Gyromagnetic Ratio

January 16, 2016

GoLuckyRyan Basic, theory dipole, gyromagnetic, Larmor, moment, NMR, spin Leave a comment

I always confuses on the definition, and wiki did not have any summary. so,

The Original definition is the Hamiltonian of a magnetic dipole under external magnetic field $\vec{B}$ ,

$H = -\vec{\mu}\cdot \vec{B}$ ,

where $\vec{\mu}$ is magnetic dipole moment (MDM). It is

$\vec{\mu} = g \frac{q}{2 m} \vec{J} = g \frac{\mu}{\hbar} \vec{J} = \gamma \vec{J}$ .

Here, the $g$ is the g-factor, $\mu$ is magneton, and $\vec{J}$ is the total spin, which has a intrinsic factor $m\hbar / 2$ inside. $\gamma$ is gyromegnetic ratio.

We can see, the g-factor depends on the motion or geometry of the MDM. For a point particle, the g-factor is exactly equal to 2. For a charged particle orbiting, the g-factor is 1.

Put everything into the Hamiltonian,

$H = -\gamma \vec{J}\cdot \vec{B} = -\gamma J_z B = -\gamma \hbar \frac{m}{2} B [J]$ ,

Because energy is also equal $E = \hbar f$ , thus, we can see the $\gamma$ has unit of frequency over Tesla.

———————————–

Take electron as an example, the MDM is Bohr magneton $\mu_{e} = e\hbar/(2m_e)$ . The MDM is,

$\vec{\mu_e} = g_e \frac{e}{2 m_e} \vec{S} = g_e \frac{\mu_e}{\hbar}\vec{S} = \gamma_e \vec{S}$ .

The magnitude of MDM is,

$|\vec{\mu_e}|= g_e \frac{e}{2 m_e} \frac{\hbar}{2} = \gamma_e \frac{\hbar}{2} [JT^{-1}]$ ,

The gyromagnetic ratio is,

$\gamma_e = g_e \frac{\mu_e}{\hbar} [rad s^{-1} T^{-1}]$ .

Since using $rad s^{-1}$ is not convenient for experiment. The gyromagnetic ratio usually divided by $2\pi$ ,

$\gamma_e = g_e \frac{\mu_e}{2\pi\hbar} [Hz T^{-1}]$ .

————————————-

To evaluate the magnitude of MDM of single particle state, which has orbital angular momentum and spin, the total spin $\vec{J} = \vec{L} + \vec{S}$ . However, the g-factor for $\vec{L}$ is difference from that for $\vec{S}$ . Thus, the MDM is not parallel to total spin. We have to use Landé Formula,

$\left< JM|\vec{V}|JM'\right> = \frac{1}{J(J+1)} \left< JM|(\vec{J}\cdot\vec{V})|JM\right> \left<JM|\vec{J}|JM'\right>$

or see wiki, sorry for my laziness.

The result is

$g=g_L\frac{J(J+1)+L(L+1)-S(S+1)}{2J(J+1)}+g_S\frac{J(J+1)-L(L+1)+S(S+1)}{2J(J+1)}$

For $J = L \pm 1/2$ ,

$g = J(g_L \pm \frac{g_S-g_L}{2L+1})$

T1 and T2 measurement

April 21, 2011

GoLuckyRyan operational NMR, spin, spin echo Leave a comment

Measuring T1 in NMR, we apply follow pulse sequence:

$\pi_x \longrightarrow \tau \longrightarrow (\pi/2)_x$

according to previous post on density matrix in operator form, we can evaluate the polarization. suppose the magnetization is pointing with the external B-field.

$\rho_R = \rho = k\sigma_z$

$\downarrow \pi_x$

$\rho_R = - k \sigma_z$

$\downarrow \tau$

$\rho_R = -k \left( 1- 2 e^{-\tau/T_1} \right) \sigma_z$

$\downarrow (\pi/2)_x$

$\rho_R = k \left( 1- 2 e^{-\tau/T_1} \right) \sigma_y$

in lab frame:

$\rho = k \left( 1-2 e^{-\tau/T_1} \right) (\sigma_y cos(\omega_0 t) - \sigma_x sin(\omega_0 t) )$

if the NMR coil is placed alone with x-axis. the magnetization is proportional to :

$\left<\sigma_x\right> = 2 k\left( 1- 2 e^{-\tau/T_1} \right) sin(\omega_0 t)$

the amplitude of the magnetization is only a function of $\tau$ . bu measuring the amplitude with different $\tau$ , we can determine the $T_1$ .

To measure the T2, we use follow pulse sequence:

$(\pi/2)_x \longrightarrow \tau \longrightarrow (\pi)_y \longrightarrow \tau$

again we use the same initial state, but this time, we are going watch it as lab frame.

$\rho = k\sigma_z$

$\downarrow (\pi/2)_x$

$\rho = - k \sigma_y$

$\downarrow \tau$

$\rho = -k (\sigma_y cos( \omega_0 \tau ) - \sigma_x sin(\omega_0 \tau) ) e^{- \tau/T_2}$

$\downarrow \pi_y$

$\rho = -k (\sigma_y cos( \omega_0 \tau ) + \sigma_x sin(\omega_0 \tau) ) e^{- \tau/T_2}$

$\downarrow \tau$

$\rho = - k \sigma_ye^{- 2 \tau/T_2}$

at the last step, the free-induction decay is not decay but a revert process of decay. we see that the state back to its beginning state! thus, this method also called the spin echo. this can be see in pictorial way. after the $(\pi/2)_x$ pulse, the spin go to – y axis. now, due to the incoherence of each spin, some spin are faster and some are slower. after a time $\tau$ , the $\pi_y$ pulse flips all the spin by 180 degree. now, the “slower” spin become ahead of the “faster” spin. After the same time interval, the “faster” spin will catch up the “slower” spin and all the spin becomes coherence at that moment again! thus, the amplitude of the signal will become large again. However, since the spins are not at same Larmor frequency, some will flip more than 180 degrees while some flip less, thus, the decay are still there.

Note:

the FID ( free induction decay) rate is not exactly equal to T2, since there are many other way to make the spin polarization decay. the FID decay rate $T_2^*$ should be :

$\frac{1}{T_2 ^*} = \frac{1}{T_2} + \frac{1}{T_{others}}$

and the spin echo method can eliminate the others.

Deuteron

February 8, 2011

GoLuckyRyan no math, Porperties, Working on 2H, Binding Energy, Coulomb, deuteron, gamma, isospin, neutron, parity, proton, spin, strong force, symmetry Leave a comment

[last update 2020-08-09]

The deuteron is the nucleus that contains 1 proton and 1 neutron. The spin and isospin of proton and neutron are the same, both are equal to half. It is the only stable state for 2 nucleons. Deuteron provides a unique place to study the inter-nuclear force. The strong force is believed to be charge independent. Thus, the strong force can be easy to study on deuteron due to the absence of other forces or eliminate from the Coulomb force, which is understood very much.

The mass of deuteron is 1876.1244 MeV. The binding energy is then 2.2245MeV. It was determined by the slow neutron capture of a proton. The emitted gamma ray is approximately equal to the binding energy and the deuteron mass was extracted.

Deuteron has no excited state. It is because any excitation will easily make the system break apart. When thinking of deuteron as one of the families of the NN system. Because of tensor force, which favors T=0 pn pair, thus only T=0, S=1 pn pair, which is deuteron is bounded. Any excitation will change the isospin from T=0 to T=1, which is unbound.

Here is a list of the experimental fact of the deuteron:

The binding energy is 2.2245 MeV (reference?)
The total spin is 1. (reference? exp?)
The magnetic dipole moment is 0.857 $\mu_N$ , where $\mu_N \frac{eh}{2 c m_N}$ is nuclear magnetron. (reference? exp?)
The electric dipole moment is 0.00282 b. (reference? exp?) In other way to view that is from the mean square values of wave function along the z-axis and all axis, i.e. $\left<z^2\right>$ and $\left<r^2\right> = \left<x^2\right> + \left<y^2\right> + \left<z^2\right>$ , the ratio between these 2 are 1.14/3, instead of 1/3.
The radius is 2.1254(50) fm [Randolf Pohl et al., J. Phys. Conf. Ser. 264, 012008 (2011)]

The parity is positive from experiment (how? ref?). If we separate the deuteron wavefunction into 3 parts. The proton wavefunction, neutron wavefunction, and the orbital wavefunction. Under the only force, the strong force in this system, proton and neutron are the same nucleon with different states. Thus, the parity is the same for proton and neutron. So, the product of these 2 wavefunctions always has positive parity. The total parity then is solely given by the angular orbital.

Any orbital wave function can be represented by the spherical harmonic, $Y(l,m)$ . The parity transform is changing it to

$Y(l,m) \rightarrow (-1)^l Y(l,m)$

So, the experimental face of positive parity fixed the angular momentum must be even.

Ok, we just predicted the possible angular momentum from parity.

The experimental fact on spin is 1. Since J = L + S, and the value of J can take every integer from |L-S| to L + S. and L must be even. The spin of proton and neutron is 1/2. Thus the possible S is 0 or 1 ( we are using L-S coupling scheme ). J = 1 = L + S , which tells us S must be odd to give out 1 for an even L. Thus S=1. So, the only possible L is 0 and 1. Thus, the possible state of the deuteron is (L,S) = (0,1) or (2,1). Therefore, a deuteron could ve a mixed state, if without any further argument.

The isospin can now be fixed by the law that 2 fermions state must be antisymmetry. The spatial state symmetry is even by L = 0 or 2. And for the state (L , S) = ( 0, 1 ), the spin state is symmetric. Thus, the isospin must be antisymmetric. Since the algebra for isospin and spin are the same. We use T = 0 for the isospin. Thus a complete wavefunction is ( L , S , T ) = ( 0 , 1, 0 ).

[20230228 updates]

The coupled equations for the radial function of the deuteron are in here.

The Argonne V18 potential for NN system is in here.

The deuteron pn-interaction from AV18 potential is here.

The deuteron radial wave function is here.

The deuteron rms mass radius, dipole moment, and quadrupole moment are here.

Optical Model II

February 7, 2011

GoLuckyRyan advance, Basic, Scattering, theory analyzing power, polarization, spin, symmetry Leave a comment

Last post on optical model, we did not include the spin. to introduced the spin, we just have to modify the wave function. For spin-½ case.

$\begin {pmatrix} \psi_i \\ \psi_2 \end {pmatrix} \rightarrow Exp( i k r ) \begin {pmatrix} a_1 \\ a_2 \end {pmatrix} + \frac { Exp ( i k r) }{r} M \begin {pmatrix} a_1 \\ a_2 \end {pmatrix}$

where the M is a matrix:

$M = f + g \vec{ \sigma } \cdot \vec{n}$

the f is for the spin-Independence part of the wave function. For the incident wave and the scattered plane wave.

$\begin {pmatrix} a_1 \\ a_2 \end {pmatrix} = \begin {pmatrix} Exp( - i \phi_s /2 ) cos ( \theta_s /2 ) \\ Exp( i \phi_s /2 ) sin ( \theta_s /2 ) \end {pmatrix}$

where $\theta_s$ and $\phi_s$ are the angle of spin . not the detector angle.

after calculation by routine algebra, we have the scattered spherical wave.

$\chi = M \cdot \begin {pmatrix} a_1 \\ a_2 \end {pmatrix} =$ $\begin {pmatrix} (f+g)Exp( - i \phi_s /2 ) cos ( \theta_s /2 ) \\ (f-g)Exp( i \phi_s /2 ) sin ( \theta_s /2 ) \end {pmatrix}$

The expectation of the wavefunction, or the intensity of the spherical part will be:

$I(\theta_s) = \chi^{\dagger} \chi = |f|^2 + |g|^2 + 2 Re( f^* g ) cos( \theta_s)$

the beam polarization should be equal the intensity and normalized polarization.

$I P_z = \chi^{\dagger} \sigma_z \chi = ( |f|^2+ |g|^2 ) cos ( \theta_s) + 2 Re(f^* g)$

Thus, we have the induced polarization when incident beam is unpolarized:

$P_z ( \theta_s = \pi /2 ) = \frac { 2 Re ( f^* g ) }{ |f|^2 + |g|^2 }$

for a beam of many particle and formed an ensemble, the $\theta_s$ is the average.

and Analyzing power, which is a short term for Polarization Analyzing Power , or the spin asymmetry, is given by

$A_y=\frac { I(\theta_s = 0 ) - I( \theta_s = \pi ) } { I ( \theta_s = 0 ) + I ( \theta_s = \pi ) } = \frac { 2 Re( f^*g) }{ |f|^2 + |g|^2 } =P_z$

Therefore, in order to get the spin asymmetry, we have to use 2 polarized beams, one is up-polarized, and another is down-polarized, to see the different between the scattering result.

However, to have 100% polarized beam is a luxury. in most cases, we only have certain polarization. thus, the spin-asymmetry is not equal to the analyzing power. the spin-asymmetry $\epsilon$ is from the yield measurement.

$\epsilon = \frac { I(\theta_s) - I(\theta_s) }{ I(\theta_s ) + I(\theta_s) }$

since f and g only depend on the detector angle. and we can assume they are symmetry. Thus

$\epsilon = \frac {2 Re( f^* g ) }{|f|^2 +|g|^2 } cos ( \theta_s) = A_y P$

the P is the polarization of the target.

Projection theorem

February 5, 2011

GoLuckyRyan advance, Spherical Stuffs, theory angular momentum, Bohr, g-factor, magneton, orbital, spin, spin-orbital, Wigner-Eckart, Zeeman Leave a comment

The simplest way to say is:

a operator can be projected on another one, for example, The orbital angular momentum cab be projected on the total angular momentum.

$L = L\cdot J \frac {J}{j(j+1)}$

a simple application is on the Zeeman effect on spin-orbital coupling. the Hamiltonian is:

$H_B = - \mu \cdot B = - ( \mu_l L + \mu_s S ) \cdot B$

by the Wigner-Eckart theorem:

$L = L\cdot J \frac {J}{j(j+1)}$

$S = S\cdot J \frac {J}{j(j+1)}$

then the Hamiltonian becomes:

$H_B = - \frac{1}{j(j+1)} ( \mu_l (L \cdot J) + \mu_s (S \cdot J) ) J\cdot B$

and introduce the Bohr Magneton and g-factor:

$H_B = - g \mu_B J \cdot B$

$g = - \frac{1}{j(j+1)} ( g_l (L \cdot J) + g_s (S \cdot J) )$

a review on Hydrogen’s atomic structure

February 2, 2011

GoLuckyRyan advance, atomic, Basic, review, theory angular, angular momentum, Coulomb, coupling, Darwin, Dirac, field, fine structure, Hamiltonian, hydrogen, hyperfine structure, Magnetic, moment, momentum, orbital, relativity, SI unit, spin, Zeeman Leave a comment

I found that most of the book only talk part of it or present it separately. Now, I am going to treat it at 1 place. And I will give numerical value as well. the following context is on SI unit.

a very central idea when writing down the state quantum number is, is it a good quantum number? a good quantum number means that its operator commute with the Hamiltonian. and the eigenstate states are stationary or the invariant of motion. the prove on the commutation relation will be on some post later. i don’t want to make this post too long, and with hyperlink, it is more reader-friendly. since somebody may like to go deeper, down to the cornerstone. but some may like to have a general review.

the Hamiltonian of a isolated hydrogen atom is given by fews terms, deceasing by their strength.

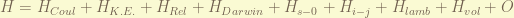
$H = H_{Coul} + H_{K.E.} + H_{Rel} + H_{Darwin} + H_{s-0} + H_{i-j} + H_{lamb} + H_{vol} + O$

the Hamiltonian can be separated into 3 classes.

__________________________________________________________

Bohr model

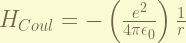
$H_{Coul} = - \left(\frac {e^2}{4 \pi \epsilon_0} \right) \frac {1}{r}$

is the Coulomb potential, which dominate the energy. recalled that the ground state energy is -13.6 eV. and it is equal to half of the Coulomb potential energy, thus, the energy is about 27.2 eV, for ground state.

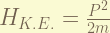
$H_{K.E.} = \frac {P^2}{ 2 m}$

is the non-relativistic kinetic energy, it magnitude is half of the Coulomb potential, so, it is 13.6 eV, for ground state.

comment on this level

this 2 terms are consider in the Bohr model, the quantum number, which describe the state of the quantum state, are

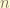$n$ = principle number. the energy level.

$l$ = orbital angular momentum. this give the degeneracy of each energy level.

$m_l$ = magnetic angular momentum.

it is reasonable to have 3 parameters to describe a state of electron. each parameter gives 1 degree of freedom. and a electron in space have 3. thus, change of basis will not change the degree of freedom. The mathematic for these are good quantum number and the eigenstate $\left| n, l, m_l \right>$ is invariant of motion, will be explain in later post. But it is very easy to understand why the angular momentum is invariant, since the electron is under a central force, no torque on it. and the magnetic angular momentum is an invariant can also been understood by there is no magnetic field.

the principle quantum number 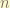$n$ is an invariance. because it is the eigenstate state of the principle Hamiltonian( the total Hamiltonian )!

the center of mass also introduced to make more correct result prediction on energy level. but it is just minor and not much new physics in it.

Fine structure

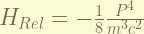
$H_{Rel} = - \frac{1}{8} \frac{P^4}{m^3 c^2}$

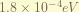is the 1st order correction of the relativistic kinetic energy. from $K.E. = E - mc^2 = \sqrt { p^2 c^2 + m^2c^4} - mc^2$ , the zero-order term is the non-relativistic kinetic energy. the 1st order therm is the in here. the magnitude is about $1.8 \times 10^{-4} eV$ . ( the order has to be recalculate, i think i am wrong. )

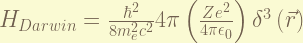
$H_{Darwin} = \frac{\hbar^{2}}{8m_{e}^{2}c^{2}}4\pi\left(\frac{Ze^2}{4\pi \epsilon_{0}}\right)\delta^{3}\left(\vec r\right)$

is the Darwin-term. this term is result from the zitterbewegung, or rapid quantum oscillations of the electron. it is interesting that this term only affect the S-orbit. To understand it require Quantization of electromagnetic field, which i don’t know. the magnitude of this term is about 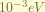$10^{-3} eV$

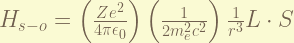
$H_{s-o} = \left(\frac{Ze^2}{4\pi \epsilon_{0}}\right)\left(\frac{1}{2m_{e}^{2}c^{2}}\right)\frac{1}{r^3} L \cdot S$

is the Spin-Orbital coupling term. this express the magnetic field generated by the proton while it orbiting around the electron when taking electron’s moving frame. the magnitude of this term is about 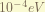$10^{-4} eV$

comment on this level

this fine structure was explained by P.M.Dirac on the Dirac equation. The Dirac equation found that the spin was automatically come out due to special relativistic effect. the quantum number in this stage are

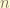$n$ = principle quantum number does not affected.

$l$ = orbital angular momentum.

$m_l$ = magnetic total angular momentum.

$s$ = spin angular momentum. since s is always half for electron, we usually omit it. since it does not give any degree of freedom.

$m_s$ = magnetic total angular momentum.

at this stage, the state can be stated by $\left| n, l, m_l, m_s \right>$ , which shown all the degree of freedom an electron can possible have.

However, 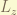$L_z$ is no longer a good quantum number. it does not commute with the Hamiltonian. so, $m_l$ does not be the eigenstate anymore. the total angular momentum was introduced $J = L + S$ . and $J^2$ and $J_z$ commute with the Hamiltonian. therefore,

$j$ = total angular momentum.

$m_j$ = magnetic total angular momentum.

an eigenstate can be stated as 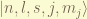$\left| n, l, s, j, m_j \right>$ . in spectroscopy, we denote it as 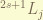$^{2 s+1} L _j$ , where $L$ is the spectroscopy notation for $l$ .

there are 5 degrees of freedom, but in fact, s always half, so, there are only 4 real degree of freedom, which is imposed by the spin ( can up and down). the reason for stating the s in the eigenstate is for general discussion. when there are 2 electrons, s can be different and this is 1 degree of freedom.

Hyperfine Structure

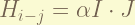
$H_{i-j} = \alpha I \cdot J$

is the nuclear spin- electron total angular momentum coupling. the coefficient of this term, i don’t know. Sorry. the nuclear has spin, and this spin react with the magnetic field generate by the electron. the magnitude is 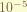$10^{-5}$

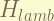
$H_{lamb}$

is the lamb shift, which also only affect the S-orbit.the magnitude is 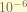$10^{-6}$

comment on this level

the hyperfine structure always makes alot questions in my mind. the immediate question is why not separate the orbital angular momentum and the electron spin angular momentum? why they first combined together, then interact with the nuclear spin?

may be i open another post to talk about.

The quantum number are:

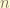$n$ = principle quantum number

$l$ = orbital angular momentum

$s$ = electron spin angular momentum.

$j$ = spin-orbital angular momentum of electron.

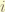$i$ = nuclear spin. for hydrogen, it is half.

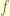$f$ = total angular momentum

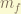$m_f$ = total magnetic angular momentum

a quantum state is $\left| n, l, s, j,i, f , m_f \right>$. but since the s and i are always a half. so, the total degree of freedom will be 5. the nuclear spin added 1 on it.

Smaller Structure

$H_{vol}$

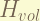
this term is for the volume shift. the magnitude is $10^{-10}$ .

in diagram:

On NMR signal

January 29, 2011

GoLuckyRyan Basic, operational, theory electromagnetism, Larmor, magnetization, NMR, Rabi, spin Leave a comment

The NMR signal is obtained by the coil, which also generate the Rabi field or a radio frequency to flip the spin.

the origin of the NMR signal is the transverse magnetization. for spin-½ system. the transverse component of the magnetization is:

$M_T = ( M_x, M_y ) = A ( cos(\omega_0 t), sin(\omega_0 t))$

where $A$ is the amplitude and $\omega_0$ is the Larmor frquency. for consistency and cross reference in this blog, i keep the 0 with the $\omega$ .

the magnetization is proportional a changing magnetic field. a changing magnetic field will induce an e.m.f on a coil. if the coil is perpendicular to an oscillating magnetic field a maximum e.m.f will be obtained. however, since the magnetization is rotating, the coil can be point at any direction to give the same e.m.f. . without lost of generality, the coil will define the x-axis of the system.

$B = B_{NMR} ( cos (\omega_0 t ), sin ( \omega_0 t) )$

and the Maxwell’s equation:

$\nabla \times E = \frac { d}{dt} B$

$\nabla \times E = B_{NMR} \omega_0 ( - sin (\omega_0 t), cos(\omega_0 t))$

we can see that the amplitude of the E field in the coil, which is the NMR signal strength, is depending on the Larmor frequency $\omega_0$ . That explained why NMR always looking for strong magnetic field, now can go to 22 Tesla ( earth magnetic field is just $5 \times 10^{-5}$ Tesla ), a higher magnetic field strength, the higher Larmor frequency, and a stronger signal.

Moreover, the magnetic field produced by the sample is proportional to number of NMR center, the polarization and a factor on how the spin ensemble to combine to be a giant single field. and also, the change of the flux of the NMR coil is depends on how the area was integrated. These all factor are not just related to the NMR coil but also on the particular sample.

detail treatment on Larmor Precession and Rabi Resonance

January 29, 2011

GoLuckyRyan Basic, review, theory angular momentum, density matrix, frame, Larmor, magnetization, NMR, precess, Rabi, relaxation, resonance, rotation, spin, transverse Leave a comment

a treatment on Larmor Precession and Rabi resonance

the pdf is a work on this topic. it goes through Larmor Precession and give example on spin-½ and spin-1 system.

then it introduce Density matrix and gives some example.

The Rabi resonance was treated by rotating frame method and using density matrix on discussion.

the last topic is on the relaxation.

the purpose of study it extensively, is the understanding on NMR.

the NMR signal is the transverse component of the magnetization.

on angular momentum adding & rotation operator

January 29, 2011

GoLuckyRyan experimental, idea, no math, Spherical Stuffs, Working on angular, degree of freedom, dimension, Larmor, momentum, orbital, positron, rotation, Sakurai, spin, temperature 2 Comments

the angular momentum has 2 kinds – orbital angular momentum $L$ , which is caused by a charged particle executing orbital motion, since there are 3 dimension space. and spin $S$ , which is an internal degree of freedom to let particle “orbiting” at there.

thus, a general quantum state for a particle should not just for the spatial part and the time part. but also the spin, since a complete state should contains all degree of freedom.

$\left| \Psi \right> = \left| x,t \right> \bigotimes \left| s \right>$

when we “add” the orbital angular momentum and the spin together, actually, we are doing:

$J = L \bigotimes 1 + 1 \bigotimes S$

where the 1 with L is the identity of the spin-space and the 1 with S is the identity of the 3-D space.

the above was discussed on J.J. Sakurai’s book.

the mathematics of $L$ and $S$ are completely the same at rotation operator.

$R_J (\theta) = Exp( - \frac {i}{\hbar} \theta J)$

where $J$ can be either $L$ or $S$ .

the $L$ can only have effect on spatial state while $S$ can only have effect on the spin-state. i.e:

$R_L(\theta) \left| s \right> = \left| s\right>$

$R_S(\theta) \left| x \right> = \left| x\right>$

the $L_z$ can only have integral value but $S_z$ can be both half-integral and integral. the half-integral value of $Sz$ makes the spin-state have to rotate 2 cycles in order to be the same again.

thus, if the different of $L$ and $S$ is just man-made. The degree of freedom in the spin-space is actually by some real geometry on higher dimension. and actually, the orbital angular momentum can change the spin state:

$L \left| s \right> = \left | s' \right > = c \left| s \right>$

but the effect is so small and

$R_L (\theta) \left| s\right > = Exp( - \frac {i}{\hbar} \theta c )\left| s \right>$

but the c is very small, but if we can rotate the state for a very large angle, the effect of it can be seen by compare to the rotation by spin.

$\left < R_L(\omega t) + R_S(\omega t) \right> = 2 ( 1+ cos ( \omega ( c -1 ) t)$

the experiment can be done as follow. we apply a rotating magnetic field at the same frequency as the Larmor frequency. at a very low temperature, the spin was isolated and $T_1$ and $T_2$ is equal to $\infty$ . the different in the c will come up at very long time measurement and it exhibit a interference pattern.

if $c$ is a complex number, it will cause a decay, and it will be reflected in the interference pattern.

if we find out this c, then we can reveal the other spacial dimension!

___________________________________

the problem is. How can we act the orbital angular momentum on the spin with out the effect of spin angular momentum? since L and S always coupled.

one possibility is make the S zero. in the system of electron and positron. the total spin is zero.

another possibility is act the S on the spatial part. and this will change the energy level.

__________________________________

an more fundamental problem is, why L and S commute? the possible of writing this

$\left| \Psi \right> = \left| x,t \right> \bigotimes \left| s \right>$

is due to the operators are commute to each other. by why?

if we break down the L in to position operator x and momentum operator p, the question becomes, why x and S commute or p and S commute?

$[x,S]=0 ?$

$[p,S]=0 ?$

$[p_x, S_y] \ne 0 ?$

i will prove it later.

___________________________________

another problem is, how to evaluate the Poisson bracket? since L and S is not same dimension. may be we can write the eigenket in vector form:

$\begin {pmatrix} \left|x, t \right> \\ \left|s\right> \end {pmatrix}$

i am not sure.

___________________________________

For any vector operator, it must satisfy following equation, due to rotation symmetry.

$[V_i, J_j] = i \hbar V_k$ run in cyclic

Thus,

where J is rotation operator. but i am not sure is it restricted to real space rotation. any way, spin is a vector operator, thus

$latex [S_x, L_y] = i \hbar S_z = – [S_y, L_x] $

so, L, S is not commute.

on Relaxation in NMR

January 28, 2011

GoLuckyRyan Basic, operational, theory density matrix, ensemble, frequency, π-pluse, Larmor, magnetization, NMR, spin Leave a comment

If we only switch on the transverse magnetic field for some time $\tau$ . after the field is off, the system will go back to the thermal equilibrium. it is due to the system is not completely isolated.

instead of consider a single spin, we have to consider the ensemble. and an ensemble is describe by the density matrix.

the reason for not consider a single spin state is, we don’t know what is going on for individual spin. in fact, in the previous section, the magnetization is a Marco effect. a single spin cannot have so many states, it can only have 2 states – up or down. if we insist the above calculation is on one spin, thus, it only give the chance for having that direction of polarization. which, is from many measurements.

so, for a single spin, the spin can only have 2 states. and if the transverse B field frequency is not equal to the Larmor frequency , and the pule is not a π-pulse, the spin has chance to go to the other state, which probability is given by a formula. and when it goes to relax back to the minimum energy state, it will emit a photon. but when it happen, we don’t know, it is a complete random process.

However, an ensemble, a collection of spins, we can have some statistic on it. for example, the relaxation time, T1 and T2.

Nuclear Physics 101

Magnetic Dipole Moment & Gyromagnetic Ratio

T1 and T2 measurement

Deuteron

Optical Model II

Projection theorem

a review on Hydrogen’s atomic structure

Bohr model

Fine structure

Hyperfine Structure

Smaller Structure

On NMR signal

detail treatment on Larmor Precession and Rabi Resonance

on angular momentum adding & rotation operator

on Relaxation in NMR

Recent Posts

Calendar

Archives

Keywords

# of Visitors

Login