detail treatment on Larmor Precession and Rabi Resonance

January 29, 2011

GoLuckyRyan Basic, review, theory , , , , , , , , , , , , Leave a comment

a treatment on Larmor Precession and Rabi resonance

the pdf is a work on this topic. it goes through Larmor Precession and give example on spin-½ and spin-1 system.

then it introduce Density matrix and gives some example.

The Rabi resonance was treated by rotating frame method and using density matrix on discussion.

the last topic is on the relaxation.

the purpose of study it extensively, is the understanding on NMR.

the NMR signal is the transverse component of the magnetization.

NMR (nuclear magnetic resonance)

January 27, 2011

GoLuckyRyan Basic, no math , , , , , , , , , , Leave a comment

NMR is a technique to detect the state of nuclear spin. a similar technique on electron spin is call ESR ( electron spin resonance)

The principle of NMR is simple.

  1. apply a B-field, and the spin will align with it due to interaction with surrounding and precessing along the B-field with Larmor frequency, and go to Boltzmann equilibrium. the time for the spin align with the field is call T1, longitudinal relaxation time.
  2. Then, we send a pule perpendicular to the B-field, it usually a radio frequency pulse. the frequency is determined by the resonance frequency, which is same as the Larmor frequency. the function of this pulse is from the B-field of it and this perpendicular B-field with perturb the spin and flip it 90 degrees.
  3. when the spin are rotate at 90 degrees with the static B-field, it will generate a strong enough signal around the coil. ( which is the same coil to generate the pule ) and this signal is called NMR signal.
  4. since the spins will be affected by its environment, and experience a slightly different precession frequency. when the time goes, they will not aligned well, some precess faster, some slower. thus, the transverse magnetization will lost and look as if it decay. the time for this is called T2, transverse relaxation time.

by analyzing the T1 and T2 and also Larmor frequency, we can known the spin, the magnetization, the structure of the sample, the chemical element, the chemical formula, and alot many others thing by different kinds of techniques.

For nuclear physics, the use of NMR is for understand the nuclear spin. for example, the polarization of the spin.

 

 

Larmor Precession (quick)

January 23, 2011

GoLuckyRyan Spherical Stuffs, theory , , , , , , , , , , , , , , , 1 Comment

Magnetic moment (\mu ) :

this is a magnet by angular momentum of charge or spin. its value is:

\mu = \gamma J

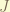where J is angular momentum, and \gamma is the gyromagnetic rato

\gamma = g \mu_B

Notice that we are using natural unit.

the g is the g-factor is a dimensionless number, which reflect the environment of the spin, for orbital angular momentum, g = 1.

\mu_B is Bohr magneton, which is equal to

\mu_B = \frac {e} {2 m} for positron

since different particle has different mass, their Bohr magneton value are different. electron is the lightest particle, so, it has largest value on Bohr magneton.

Larmor frequency:

When applied a magnetic field on a magnetic moment, the field will cause the moment precess around the axis of the field. the precession frequency is called Larmor frequency.

the precession can be understood in classical way or QM way.

Classical way:

the change of angular momentum is equal to the applied torque. and the torque is equal to the magnetic moment  cross product with the magnetic field. when in classical frame, the angular momentum, magnetic moment, and magnetic field are ordinary vector.

\vec {\Gamma}= \frac { d \vec{J}}{dt} = \vec{\mu} \times \vec{B} = \gamma \vec {J} \times \vec{B}

solving gives the procession frequency is :

\omega = - \gamma B

the minus sign is very important, it indicated that the J is precessing by right hand rule when \omega >0 .

QM way:

The Tim dependent Schrödinger equation (TDSE) is :

i \frac {d}{d t} \left| \Psi\right> = H \left|\Psi\right>

H is the Hamiltonian, for the magnetic field is pointing along the z-axis.

H = -\mu \cdot B = - \gamma J\cdot B = -gamma B J_z = \omega J_z

the solution is

\left|\Psi(t) \right> = Exp( - i \omega t J_z) \left| \Psi(0) \right>

Thus, in QM point of view, the state does not “rotate” but only a phase change.

However, the rotation operator on z-axis is

R_z ( \theta ) = Exp( - i \frac {\theta}{\hbar} J_z )

Thus, the solution can be rewritten as:

\left|\Psi (t)\right> = R_z( \omega t) \left|\Psi(0)\right>

That makes great analogy on rotation on a real vector.

Spin

January 22, 2011

GoLuckyRyan Basic, no math, Porperties, Spherical Stuffs, Working on , , , , , , , , , , , Leave a comment

( this is just a draft, not organized )

Spin is a intrinsics property of elementary particle, such as electron, proton, and even photon. Intrinsics means it is a built-in property, like mass, charge. Which extrinsic properties are speed, momentum.

Spin is a vector or tensor quality while charge and mass are scaler.

Spin can react with magnetic field, like charge reacts with electric field or mass react with force produce acceleration. Thus, spin is like a bar-magnet inside particle, counter part of charge.

The magnitude of spin is half integer or integer of reduced Planck’s constant \hbar . Particles with half integer of spin are classified as Fermion, and those with integer spin are Boson. they follow different statistic while interact together, thus, this creates different physics for different group.

we are not going to the mathematic description this time.

the effect of spin causes the magnetic moment, that’s why it react with magnetic field. the other thing that creates magnetic moment is angular momentum for charge particle, like electron orbiting around nucleus. So, both spin and angular momentum can be imagined as a little magnet, thus, they can interact, in physics, we call the interaction between spin and angular momentum is coupling. for example, spin-orbital coupling, spin-spin coupling, etc..

when the spin interact with external magnetic field, it will precess around the magnetic field with Larmor frequency. and the direction of the spin while undergoes procession can only be certain angle. for spin half, like electron or proton. there are only 2 directions, and we called it up and down.