Variational method | Nuclear Physics 101

Variational method for Woods-Saxon potential

August 31, 2021

GoLuckyRyan Basic Hankel, Runge-Kutta, Schrödinger equation, spherical Bessel, Variational method Leave a comment

In the past, we solved the radial wavefunction for the Woods-Saxon potential by Runge-Kutta method. But there is another method based on linear algebra, that all wave function can be expanded as a linear combination of a set of basis. In here, we use a free wave as basis, which is the spherical Bessel function.

to be annoying due to my poor memory , lets state the Schrödinger equation again,

$\displaystyle \left( -\frac{\hbar^2}{2m}\nabla^2 + V(r) \right)\Psi = E\Psi$

Separating the radial part

$\displaystyle \left( -\frac{\hbar^2}{2m} \frac{1}{r^2} \left( \frac{d}{dr} r^2 \frac{d}{dr} \right) +\frac{\hbar^2}{2m} \frac{l(l+1)}{r^2}+ V(r) \right) R(r) = E R(r)$

replace $R(r) = u(r) /r$

$\displaystyle \frac{1}{r^2} \left( \frac{d}{dr} r^2 \frac{d}{dr} \right) \frac{u(r)}{r} = \frac{1}{r}\frac{d^2}{dr^2} u(r)$

$\displaystyle \left( -\frac{\hbar^2}{2m} \frac{d^2}{dr^2} + \frac{\hbar^2}{2m} \frac{l(l+1)}{r^2} + V(r) \right) u(r) = E u(r)$

simplify

$\displaystyle \left( \frac{d^2}{dr^2} - \frac{l(l+1)}{r^2} - \frac{2m}{\hbar^2} V(r) \right) u(r) = -\frac{2m}{\hbar^2}E u(r)$

We can define a “free wave” Hamiltonian as

$\displaystyle \left( \frac{d^2}{dr^2} - \frac{l(l+1)}{r^2} \right) u(r) = H_0 u(r) = -k^2 u(r)$

In this post, we explored the orthogonality of the the Riccati-Bessel function, and it is the eigen state for $H_0$ with eigenvalue of $-k_n^2$ .

$\displaystyle b_k(r) = \sqrt{\frac{2}{pi}} \hat{j_l}\left(k r\right), ~~~ H_0 b_k(r) = -k^2 b_k(r)$

$\displaystyle \left< b_k | b_k' \right> = \delta(k-k')$

Thus, the Riccati-Bessel function can be served as the set of basis functions that span the whole space.

The total Hamiltonian is then

$\displaystyle \left( -\frac{\hbar^2}{2m} \frac{d^2}{dr^2} + \frac{\hbar^2}{2m} \frac{l(l+1)}{r^2} + V(r) \right) u(r) \\~~~~~~~~~~~~~~~~= \left( -\frac{\hbar^2}{2m} H_0 + V(r) \right) u(r) = E u(r)$

Since the solution can be expressed as a linear combination of the basis functions, then

$\displaystyle u(r) = \sum_n a_n b_n(r)$

$\displaystyle \left( -\frac{\hbar^2}{2m} H_0 + V(r) \right) \sum_n a_n b_n(r) = E\sum_n a_n b_n(r)$

Multiple $b_m(r)$ and integrate,

$\displaystyle \sum_{n} a_n \left< b_m \left| -\frac{\hbar^2}{2m}H_0 + V(r) \right|b_n \right> = E a_m$

The above is a matrix equation

$\displaystyle \left< -\frac{\hbar^2}{2m} H_0 + V(r) \right> \vec{a} = E \vec{a}, ~~ \vec{a} = (a_1, a_2,... a_N)$

Everything seems OK. But when I test the theory using Mathematica, it fail. For simplicity, we use the s-orbital, and the basis is

$\displaystyle b_n(r) = \sqrt{\frac{2}{\pi}} \sin\left( \frac{2\pi}{a} n r\right)$

The Woods-Saxon parameters are $V_0 = -50 \mbox{MeV}, V_{so} = 22 \mbox{MeV}, R_0 = R_{so} = 4 \mbox{fm}, a_0 = a_{so} = 0.67 \mbox{fm}$ .

Using Runge-Kutta method, the ground state energy is -36.09 MeV, and the wave function is

We set $a = 40~\mbox{fm}$ , and $n = 1, 2, ...., 40$ . The matrix elements is

$\displaystyle \left<n \left| -\frac{\hbar^2}{2m_n}H_0 + V(r) \right| m \right> = \delta_{nm} \frac{\hbar^2 k^2}{2m_n} + \left<V(r) \right>, ~~ k = \frac{2\pi}{a} n$

where $m_n$ is neutron mass.

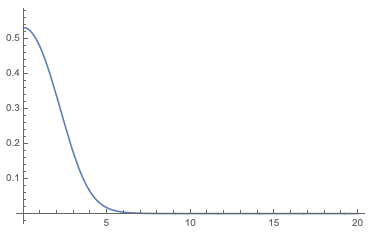
After calculate the matrix, find the eigenvalue and eigenstate. The lowest eigen energy is -465.18 MeV, which indicate something wrong. And the wave function, constructed by the eigenstate look likes

Ground state constructed by basis functions

The shape of the wavefunction looks similar to the correct wavefunction, but narrower and larger amplitude.

The next eigen wave function also look like 1s-orbital. The spectrum of the eigenvalues, which are the eigen energies, has 7 bound states.

I don’t know the problems….

One possible reason could be that the basis function is always $b_n(a) = 0$ , but the real solution is not necessary to be $\psi(a) = 0$ . In fact, the 0s-wave function never be zero except $r= 0$ .

I use the same basis and extract the coefficient,

$\displaystyle \psi(r) \approx \sum_{n}^{40} C_n \frac{\sin(k_n r)}{r}, ~ C_n = \int_0^\infty \psi(r) \sin(k_n r) r dr, ~ k_n = \frac{2\pi}{a}n$

And it can reproduce the original wave function at $r < 10 \mbox{fm}$

Since the basis function is a sine wave and we only sum limited term, the long range oscillation can not be suppressed.

Another possible reason is that the basis is not normalizable. This root at the orthogonality of Bessel function that

$\displaystyle \int_0^\infty J_\nu^2(kx) x dx = \infty$

An-another possible reason is that, the basis is for unbound state. But in this post, we used a not-normalizable, unbounded basis to construct the bound state wave function. It can form the solution correctly at short-range, but it is periodic. This is the nature of series expansion, always periodic.

In this sense, we are also expanding the solution into a series, that the series only produce periodic function, therefore, a correct way to do is using the spherical Hankel transform, which is transform the Schrodinger equation into momentum space.

Nilsson Orbital using diagonalization method

July 25, 2019

GoLuckyRyan Basic Clebsch-Gordon, diagonalization, Harmonic Oscillator, harmonics, Laguerre polynomial, Nilsson orbital, Variational method Leave a comment

Long time ago, I tried to tackle the Nilsson orbital by solving the Hamiltonian analytically. However, the Hamiltonian is without LS coupling. This times, I redo the calculation according to the reference B. E. Chi, Nuclear Phyiscs 83 (1966) 97-144.

The Hamiltonian is

$\displaystyle H = \frac{P^2}{2m} + \frac{1}{2}m\left( \omega_\rho^2 (x^2+y^2) + \omega_z^2 z^2 \right) + C L\cdot S + D L\cdot L$

using

$\displaystyle \omega_\rho = \omega_0 \left(1+\frac{2}{3}\delta\right)^{\frac{1}{2}} = \omega \left(\frac{3+2\delta}{3-4\delta}\right)^{1/6}$

$\displaystyle \omega_z = \omega_0 \left(1-\frac{4}{3}\delta\right)^{\frac{1}{2}} = \omega \left(\frac{3-4\delta}{3+2\delta}\right)^{1/3}$

$\displaystyle \beta = \frac{4}{3}\sqrt{\frac{\pi}{5}}\delta$

$\displaystyle r^2 Y_{20}(\theta, \phi) = \frac{1}{4}\sqrt{\frac{5}{\pi}} (3z^2-r^2)$

The Hamiltonian becomes

$\displaystyle H = -\frac{\hbar^2}{2m}\nabla^2 +\frac{1}{2} m \omega_0^2 r^2 - \frac{1}{2} m\omega_0^2 r^2 \beta Y_{20} + C L\cdot S + D L\cdot L$

Set $x_i^2 \rightarrow x_i^2 \frac{\hbar}{m \omega_0}$ , and $r^2 \rightarrow \rho^2 \frac{\hbar}{ m \omega_0}$

$\displaystyle \frac{H}{\hbar\omega_0} = \frac{1}{2}(-\nabla^2 + \rho^2) - \rho^2 \beta Y_{20} - 2 \kappa L\cdot S - \mu \kappa L\cdot L$

Set

$\displaystyle \frac{H_0}{\hbar\omega_0} = \frac{1}{2}(-\nabla^2 + \rho^2) - 2 \kappa L\cdot S - \mu \kappa L\cdot L$

and the perturbation is

$\displaystyle \frac{H_p}{\hbar\omega_0} = - \rho^2 Y_{20}$

with

$\displaystyle \hbar \omega_0 \approx 45 A^{-1/3} - 25 A^{-2/3}$

For example, when A = 12, $\hbar \omega_0 \approx 15$ MeV, when A = 132, $\hbar \omega_0 \approx 8$ MeV

The wavefunction for the spherical harmonic is

$\displaystyle |Nljk\rangle = A r^l e^{-\frac{r^2}{2}} L_{\frac{N-l}{2}}^{l + \frac{1}{2}}(r^2) \sum_{m m_s} Y_{lm}(\theta, \phi) \chi_{\frac{1}{2} m_s} C_{lm\frac{1}{2} m_s}^{jk}$

$\displaystyle A = \sqrt{\frac{(\frac{N-l}{2})!(\frac{N+l}{2})! 2^{N+l+2}}{\sqrt{\pi} (N+l+1)!}}$

The diagonal elements are

$\displaystyle \frac{1}{\hbar \omega_0 }\langle Nljk|H_0|Nljk\rangle = N + \frac{3}{2} - \kappa \langle L\cdot S \rangle - \mu \kappa l(l+1)$

where $\langle L \cdot S \rangle = \frac{1}{2} ( j(j+1) - l(l+1) - \frac{3}{4} )$

The off diagonal elements are

$\displaystyle \frac{1}{\hbar \omega_0 }\langle Nljk|H_p|Nljk\rangle = - \langle Nljk| r^2 Y_{20}|Nljk\rangle$

( I will evaluate this integral in future )

The rest is diagonalization the Hamiltonian

$\displaystyle H = H_0 + \beta H_p$

Here is the calculation for the 2nd harmonic for $\kappa = 0.05, \mu = 0$

Screen Shot 2019-07-25 at 18.25.45.png

The component of each orbital can be directly taken from the eigenvalue. Here is the [521]1/2 state. $\kappa = 0.05, \mu(N=3) = 0.35, \mu(N=4) = 0.625, \mu(N=5) = 0.63$

Screen Shot 2019-07-25 at 18.28.27.png

Hartree method for 1D infinite potential well

October 7, 2017

GoLuckyRyan theory Eigen System, Hartree-Fock, Schrödinger equation, Variational method Leave a comment

In order to test my understanding on the Hartree method. I played a simple case. The potential is

$V(x) = \left\{ \begin{matrix} 0 , 0 \leq x \leq \pi \\ \infty , else \end{matrix} \right\}$

The mutual interaction between 2 particles is, for simple calculation,

$G(x_1, x_2) = g_0 \cos(x_1 - x_2)$

This mutual interaction is repulsive, we can expect the eigen wave function will be more spread out.

We use the eigen state of the $V(x)$ potential to be the basis,

$\displaystyle \phi_n(x) = \sqrt{\frac{2}{\pi}} \sin(nx)$

The Hartree method is basically solving the Hartree equation

$\displaystyle \left( -\frac{\hbar^2}{2m} \frac{d^2}{dx_1^2} + V(x_1) + \int G(x_1, x_2) (\psi_k(x_2))^2 dx_2 \right) \psi_n(x_1) = \epsilon_n \psi_n(x_1)$

We assume the two particles are in the same ground state, thus, $k = n = 1$ . We assume,

$\psi_1(x) = \sum a_i \phi_i(x)$

The algorithm is that, for the 1 particles matrix

$\displaystyle F_{ij} = \int \psi_i(x) \left( -\frac{\hbar^2}{2m} \frac{d^2}{dx^2} + V(x) \right) \psi_j(x) dx$

Define

$\displaystyle G_0(x) = \int G(x, x_2) (\psi_1(x_2))^2 dx_2$

The 2-particle matrix

$\displaystyle G_{ij} = \int \psi_i(x) G_0(x) \psi_j(x) dx$

For the 1st trial, we set

$\psi_i^{(0)}(x) = \phi_{(2i+1)}(x)$

We only use “even” function with respect to $x = \pi/2$ , because mixing parity will result non-reasonable result. ( why ? )

Then we get the matrix of the Hartree Hamiltonian $H_{ij} = F_{ij} + G_{ij}$ , and solve for the eigen value and eigen vector,

$\vec{v}^{(0)} = (v_1^{(0)}, v_2^{(0)}, .... v_n^{(0)})$

The next trial is

$\displaystyle \psi_i^{(1)}(x) = \sum_i v_i^{(0)} \psi_i^{(0)}$

The process repeated until converge. The convergent can be exam using the Hartree Hamiltonian that the non-diagonal terms are vanished, i.e.

$F_{ij} + G_{ij} = 0, i\neq j$

I tried with 2 basis and 6 basis, I set $\hbar^2/2m = 1$ for simplicity, the Hartree ground state is 1.7125 for both basis. The eigen wavefunction for the 2-basis is

$\psi(x) = 0.797752 \sin(x) + 0.0145564 \sin(3x)$

with the mean field

$V_m(x) = 0.842569 \sin(x)$

For 6 basis, the wave function is

$\psi(x) = 0.797751 \sin(x) + 0.0145729 \sin(3 x) + 0.000789143 \sin(5 x) + 0.000125871 \sin(7 x) + 0.0000336832 \sin(9 x) + 0.0000119719 \sin(11 x)$

we can see, the contribution of the higher energy states are getting smaller and smaller. The higher energy states only contributes 0.03%. Following is the plot compare $\phi_1(x)$ (orange) and $\psi(x)$ (blue). We can see that the wave function becomes little spread out.

If we increase the strength of the mutual interaction by 10 times, the wave function becomes more spread out.

To cross check the result, we can use the mean field and solve the Schrodinger equation using variational method. The method gives the ground state energy be 1.7125 and converge.

This is interesting that the variational method needs 4 or 5 basis to converge, while Hartree method only need 2.

At last, we substitute the wave functon back to the Hartree equation, it turns out the result is not satisfied 100%. The total wave function is

$\Psi(x_1, x_2) = \psi(x_1) \psi(x_2)$

The Schrodinger equation is

$\displaystyle H \Psi = -\frac{\hbar^2}{2m}\left(\frac{d^2}{dx_1^2} + \frac{d^2}{dx_2^2}\right) \Psi(x_1,x_2) + G(x_1,x_2)\Psi(x_1,x_2) = E \Psi(x_1,x_2)$

However, the left side and the right side are not equal, but the integration

$\langle \Psi |H|\Psi\rangle = \langle |\Psi|\Psi \rangle$

is equal.

I plot the $\Psi H\Psi$ (orange) and $ E \Psi^2 $ (blue), and there difference is the following

We can imagine, the integration of the bottom plot is zero. I don’t know the reason, but I guess it is not because of the number of basis, because the higher energy states only contributes for 0.03%. I guess, it is because of the energy is the quantity that is optimized rather then the wave function. And I am not sure that the reverse of the following is true.

For the case of many particles, the $G_0$ has to sum over all other particle. When all particles are in the same states, the sum is simple. For particles distribute among different states, in general, the sum is

$\displaystyle G_0 =\sum_{k\neq i} \int G(x_1,x_2) \psi_k(x_2)^2 dx$

Here, the sum is excluded the particle $x_1$ , which is in state $i$ . For example, if the system consists of 2 particles on state-1, and 2 particles on state-2. The mean field for the particle in state-1 is constructed using 1 particles on state-1 and 2 particles on state-2. Thus the energy for the state-2 may be not correct.

The mean field for the particle on state-2, the mean field should be constructed by 2 particles on state-1 and 1 particle on state-2.

For higher states that without particle, the mean field is built by 2 particles on state-1 and 2 particles on state-2.

In general, the mean field is constructed using other particles.

This fixed mean field method is simple but we have to define the mean field for each state and calculate again and again.

Variational method on 1D potential well using plane wave basis

October 5, 2017

GoLuckyRyan Basic Eigen System, Variational method Leave a comment

in this post, we explained the principle of the variational method, and now, we apply this to a simple 1-D potential.

The potential is

$V(x) = \left \{ \begin{matrix} - V_0 & , -L/2 \leq x \leq L/2 \\ 0 & , else \end{matrix} \right \}$

The exact solution can be solved by matching boundary condition.

$\tan(\sqrt{\frac{2m}{\hbar^2}(E+V_0 ) \frac{L}{2}}) = \sqrt{\frac{|E|}{E+V_0}}$

The plane wave basis is

$b_n(x) =\frac{1}{\sqrt{a}} \exp\left( i \frac{2\pi}{a} n x \right)$

The matrix of the Hamiltonian is

$\displaystyle H_{ij} = \langle b_i | \frac{P^2}{2m} + V(x) | b_j \rangle$

$\displaystyle \langle b_i | \frac{P^2}{2m} | b_j \rangle = \delta_{ij} \frac{L}{a}\frac{\hbar^2}{2m} \left(\frac{2\pi}{a}\right)^2 i^2$

$\displaystyle \langle b_i | V(x) | b_j \rangle = -V_0 \frac{L}{a} \frac{\sin( \pi (i-j) L/a)}{\pi (i-j) L/a}$

Then, we solve for the eigen system.

I use mathematica for solving the eigen system.

For simplicity, I set $\hbar = 1, m= 1, L = 2, V_0 = 1$ . The exact solution is $E = -0.603898$ .

The parameter $a$ controls the wavelength of the plane wave. By increasing the number of wave $n$ , we effectively control the minimum wavelength $\lambda_0 = a/n$ Therefore, larger the $n$ , the energy will approach to the actual value.

I generated $a$ from 10 to 200 with step 10, and $n$ from 5 to 60 with step 5. Here is the result. As we can see, the larger the $a$ , we need more number of wave to go to the actual energy. When small $a$ and large $n$ , the result quickly converge to the actual energy. For $n = 60, a = 40$ , the energy is $E = -0.603792$ , the difference is $\Delta E = 0.000106$ or 0.02% difference.

The following plot show $a = 40$

However, when the $a$ is too small, the plane wave cannot describe the long wavelength behaviour of the actual wave function, then the converge fail. The following plot show $n = 60$

To investigate, I plot the case for $a = 3$ and $a = 10$ .

We can see, since the well width is 2, if the maximum wavelength is only 3, then it cannot capture a longer wavelength component. And we can see the calculated wave functions are repeated.