momentum | Nuclear Physics 101

Hankel Transform

May 6, 2021

GoLuckyRyan Basic Bessel function, momentum, spherical Bessel Leave a comment

I recently found out that the transformation from radial wave function to momentum radial wave function is the Hankel Transform in special case.

The Hankel transform is defined as

$\displaystyle F_\nu(k) = H_\nu(f(r)) = \int_{0}^{\infty} f(r) J_\nu(kr) r dr$

where $J_\nu(x)$ is the Bessel function J.

Since the Bessel function and the spherical Bessel function is related as

$\displaystyle j_l(x) = \sqrt{\frac{\pi}{2 x}} J_{l+1/2}(x)$

Set $\nu = l + 1/2$

$\displaystyle H_{l+1/2}(f(r)) = \sqrt{\frac{2k}{\pi}} \int_{0}^{\infty} f(r) \sqrt{r} \sqrt{\frac{\pi}{2 k r}} J_{l+1/2}(kr) r dr \\ = \sqrt{\frac{2k}{\pi}} \int_{0}^{\infty} f(r) \sqrt{r} j_l(kr) r dr$

Thus the transformation from spatial function to momentum function is

$\displaystyle \psi(k) = \sqrt{\frac{2}{\pi}}\int_0^\infty \psi(r) j_l(kr ) r^2 dr = \frac{1}{\sqrt{k}} H_{l+1/2}( \psi(r) \sqrt{r} )$

The Hankel transform is a built-in function in Mathemtica

HankelTransform[ f(r) sqrt[r], r, k, l+1/2 ] / sqrt[k]

And also the inverse Hankel transform

InverseHankelTransfrom[ F[k] sqrt[k], k, r, l+1/2 ] / sqrt[r]

But the built-in Hankel transform does not support digitized data.

Momentum distribution From Woods-Saxon potential

April 5, 2021

GoLuckyRyan Basic 15C, C++, momentum, Woods-Saxon Leave a comment

In this post, we derived the transformation between radial distribution and momentum distribution. This is a simple “Fourier Transform” in 3D with spherical Bessel function. In that post we also plot some simple functions.

The effective potential for most nuclei can be approximated (or well described) using the Woods-Saxon potential. Here we study the 15C, find the radial wave functions and the corresponding momentum distributions.

There are many way to calculate the radial function for a give set of Woods-Saxon parameters, using C++ code, MS excel, or Mathematica. In this post, I will use Mathematica. I found that MS Excel has the Bessel function, but it only accept integer n, but spherical Bessel needs half integer n, so it is not easy for calculating the momentum distribution.

In Mathematica, solving the Schrodinger equation for the radial part is extremely easy, for give energy $T$ , angular momentum $L$ , total spin $J$

sol = NDSolve[{u''[
r] == (2 m)/hbar^2 (V0/(1 + Exp[(r - R0)/a0]) - 
1/r (Exp[(r - RSO)/aSO] VSO)/(a0 (1 + Exp[(r - RSO)/aSO)]^2)
LS - T) u[r] + (L (L + 1))/r^2 u[r], u[0] == 0, u'[0] == 1}, 
u, { r, 0, 30}];

where $V_i$ is the potential depth in MeV, $R_i$ is the hald-radius in fm, $a_i$ is the diffusiveness parameter in fm, and the subscript $i$ for central and spin-orbit. $LS =( J(J+1) - L(L+1) - 3/4)/2$ is the LS coupling factor. $u(r) =r \phi(r)$ is the reduced radial function.

The normalization of the reduced radial function $u(r)$ is

$\displaystyle \int_{0}^{\infty} u(r)^2 dr = 1$

Usually, we don’t know the energy for a give state, we have to scan through all possible energy from $(V_0 , 0 )$ . When the energy $T$ is not the eigen energy, the tail of the wave function will diverge and oscillate with respect to the energy. Thus, we can use this property to find the eigen energy that the tail of the wave function is flat.

In here, I am requiring the sum $u(20) + u(30)$ to be minimum.

For 15C, the single particle energies for the 1s1/2 and 0d5/2 is known from the 14C(d,p) reaction, which are -1.2181 MeV and -0.4741 MeV, respectively.

After searching for best fit parameters, I found

$V_0 = -45.8, r_0 = 1.24, a_0 = 0.67, V_{SO} = 14.5, r_{SO} = r_0, a_{SO} = a_0$

are best fit. The energies of different states are:

Orbital	Energy (WS) [MeV]	Energy (exp) [MeV]
0s1/2	-25.634
0p3/2	-12.522
0p1/2	-10.351
1s1/2	-1.210	-1.2181
0d5/2	-0.463	-0.474

And, I have the radial function.

We can see that, the 1s1/2 orbital has largest radial distribution and the 0s1/2 has the smallest.

Next, we transform the radial distribution to the momentum distribution. The unit conversion is that

$\displaystyle k = \left[\frac{1}{fm}\right]= 197.326 [MeV/c]$

In the above figure, we scaled the distribution so that they have similar magnitude. We can see, the momentum distribution is smallest for the 1s1/2 as expected.

It is interesting that the momentum spread of the 0s1/2 and 1s1/2 are very different, the spread of the 0s1/2 is almost 3 times more than that of the 1s1/2, and that of the p-wave also about double.

And the d-wave momentum distribution has 2 bumps, this looks something wrong. (??? I am no solid answer for that. I suspect this is related to the tail of the wave function, when the tail is not zero, the spherical Bessel J times r^2 will magnify the tail. )

The radial solution of the Woods-Saxon potential (or the Schrodinger equation?) for the bound state is always take this form:

$\displaystyle R_{nl}(r) = r^{l} \exp(-\kappa r) f_{nl}(r)$

where $r^l$ is the short range behaviour, $\exp(-\kappa r), \kappa^2 \hbar^2 = 2m |E|$ is the long range behaviour, and $f_{nl}(r)$ is a modifier for the middle part of the function.

Lets assume the $f_{nl}(r) = 1$ for simplicity.

The momentum distribution using this simplified radial function is

$\displaystyle \psi_l(k) = (l+1)!2^{l+1} \kappa \frac{k^l}{(k^2+\kappa^2)^{l+2}}$

Normalized with $\int \psi_l(k)^2 dk =1$

$\displaystyle \psi_l(k) = \sqrt{\frac{2 \kappa^{l+7/2} \Gamma(2l+4)}{\Gamma(l+1/2)\Gamma(l+7/2)} } \frac{k^l}{(k^2+\kappa^2)^{l+2}}$

Here are the plot with $\kappa = 1$ for

$\displaystyle \phi_l(r) = \sqrt{ \frac {(2\kappa)^{2l+3}} {(2l+2)!} } r^l \exp(-\kappa r), \int \phi_l(r)^2 r^2 dr = 1$

the $\phi_l(r)$ is similar to $n = 1$ orbital.

The momentum distribution is good for distinguish $l = 0$ and $l = 1$ , but not so good for higher $l$ .

And it is counter intuitive that more spread of the radial function, the momentum distribution also spread out more. I guess the effect of the angular momentum has to take into account. For same $l$ , more spread of momentum still means the radial spread is smaller.

a review on Hydrogen’s atomic structure

February 2, 2011

GoLuckyRyan advance, atomic, Basic, review, theory angular, angular momentum, Coulomb, coupling, Darwin, Dirac, field, fine structure, Hamiltonian, hydrogen, hyperfine structure, Magnetic, moment, momentum, orbital, relativity, SI unit, spin, Zeeman Leave a comment

I found that most of the book only talk part of it or present it separately. Now, I am going to treat it at 1 place. And I will give numerical value as well. the following context is on SI unit.

a very central idea when writing down the state quantum number is, is it a good quantum number? a good quantum number means that its operator commute with the Hamiltonian. and the eigenstate states are stationary or the invariant of motion. the prove on the commutation relation will be on some post later. i don’t want to make this post too long, and with hyperlink, it is more reader-friendly. since somebody may like to go deeper, down to the cornerstone. but some may like to have a general review.

the Hamiltonian of a isolated hydrogen atom is given by fews terms, deceasing by their strength.

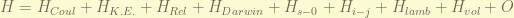
$H = H_{Coul} + H_{K.E.} + H_{Rel} + H_{Darwin} + H_{s-0} + H_{i-j} + H_{lamb} + H_{vol} + O$

the Hamiltonian can be separated into 3 classes.

__________________________________________________________

Bohr model

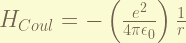
$H_{Coul} = - \left(\frac {e^2}{4 \pi \epsilon_0} \right) \frac {1}{r}$

is the Coulomb potential, which dominate the energy. recalled that the ground state energy is -13.6 eV. and it is equal to half of the Coulomb potential energy, thus, the energy is about 27.2 eV, for ground state.

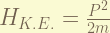
$H_{K.E.} = \frac {P^2}{ 2 m}$

is the non-relativistic kinetic energy, it magnitude is half of the Coulomb potential, so, it is 13.6 eV, for ground state.

comment on this level

this 2 terms are consider in the Bohr model, the quantum number, which describe the state of the quantum state, are

$n$ = principle number. the energy level.

$l$ = orbital angular momentum. this give the degeneracy of each energy level.

$m_l$ = magnetic angular momentum.

it is reasonable to have 3 parameters to describe a state of electron. each parameter gives 1 degree of freedom. and a electron in space have 3. thus, change of basis will not change the degree of freedom. The mathematic for these are good quantum number and the eigenstate $\left| n, l, m_l \right>$ is invariant of motion, will be explain in later post. But it is very easy to understand why the angular momentum is invariant, since the electron is under a central force, no torque on it. and the magnetic angular momentum is an invariant can also been understood by there is no magnetic field.

the principle quantum number 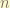$n$ is an invariance. because it is the eigenstate state of the principle Hamiltonian( the total Hamiltonian )!

the center of mass also introduced to make more correct result prediction on energy level. but it is just minor and not much new physics in it.

Fine structure

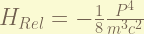
$H_{Rel} = - \frac{1}{8} \frac{P^4}{m^3 c^2}$

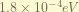is the 1st order correction of the relativistic kinetic energy. from $K.E. = E - mc^2 = \sqrt { p^2 c^2 + m^2c^4} - mc^2$ , the zero-order term is the non-relativistic kinetic energy. the 1st order therm is the in here. the magnitude is about $1.8 \times 10^{-4} eV$ . ( the order has to be recalculate, i think i am wrong. )

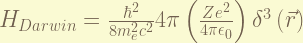
$H_{Darwin} = \frac{\hbar^{2}}{8m_{e}^{2}c^{2}}4\pi\left(\frac{Ze^2}{4\pi \epsilon_{0}}\right)\delta^{3}\left(\vec r\right)$

is the Darwin-term. this term is result from the zitterbewegung, or rapid quantum oscillations of the electron. it is interesting that this term only affect the S-orbit. To understand it require Quantization of electromagnetic field, which i don’t know. the magnitude of this term is about 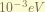$10^{-3} eV$

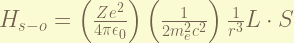
$H_{s-o} = \left(\frac{Ze^2}{4\pi \epsilon_{0}}\right)\left(\frac{1}{2m_{e}^{2}c^{2}}\right)\frac{1}{r^3} L \cdot S$

is the Spin-Orbital coupling term. this express the magnetic field generated by the proton while it orbiting around the electron when taking electron’s moving frame. the magnitude of this term is about 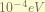$10^{-4} eV$

comment on this level

this fine structure was explained by P.M.Dirac on the Dirac equation. The Dirac equation found that the spin was automatically come out due to special relativistic effect. the quantum number in this stage are

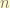$n$ = principle quantum number does not affected.

$l$ = orbital angular momentum.

$m_l$ = magnetic total angular momentum.

$s$ = spin angular momentum. since s is always half for electron, we usually omit it. since it does not give any degree of freedom.

$m_s$ = magnetic total angular momentum.

at this stage, the state can be stated by $\left| n, l, m_l, m_s \right>$ , which shown all the degree of freedom an electron can possible have.

However, 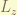$L_z$ is no longer a good quantum number. it does not commute with the Hamiltonian. so, $m_l$ does not be the eigenstate anymore. the total angular momentum was introduced $J = L + S$ . and $J^2$ and $J_z$ commute with the Hamiltonian. therefore,

$j$ = total angular momentum.

$m_j$ = magnetic total angular momentum.

an eigenstate can be stated as 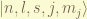$\left| n, l, s, j, m_j \right>$ . in spectroscopy, we denote it as 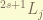$^{2 s+1} L _j$ , where $L$ is the spectroscopy notation for $l$ .

there are 5 degrees of freedom, but in fact, s always half, so, there are only 4 real degree of freedom, which is imposed by the spin ( can up and down). the reason for stating the s in the eigenstate is for general discussion. when there are 2 electrons, s can be different and this is 1 degree of freedom.

Hyperfine Structure

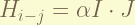
$H_{i-j} = \alpha I \cdot J$

is the nuclear spin- electron total angular momentum coupling. the coefficient of this term, i don’t know. Sorry. the nuclear has spin, and this spin react with the magnetic field generate by the electron. the magnitude is 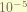$10^{-5}$

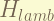
$H_{lamb}$

is the lamb shift, which also only affect the S-orbit.the magnitude is 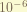$10^{-6}$

comment on this level

the hyperfine structure always makes alot questions in my mind. the immediate question is why not separate the orbital angular momentum and the electron spin angular momentum? why they first combined together, then interact with the nuclear spin?

may be i open another post to talk about.

The quantum number are:

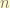$n$ = principle quantum number

$l$ = orbital angular momentum

$s$ = electron spin angular momentum.

$j$ = spin-orbital angular momentum of electron.

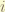$i$ = nuclear spin. for hydrogen, it is half.

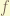$f$ = total angular momentum

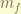$m_f$ = total magnetic angular momentum

a quantum state is $\left| n, l, s, j,i, f , m_f \right>$. but since the s and i are always a half. so, the total degree of freedom will be 5. the nuclear spin added 1 on it.

Smaller Structure

$H_{vol}$

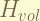
this term is for the volume shift. the magnitude is $10^{-10}$ .

in diagram:

on angular momentum adding & rotation operator

January 29, 2011

GoLuckyRyan experimental, idea, no math, Spherical Stuffs, Working on angular, degree of freedom, dimension, Larmor, momentum, orbital, positron, rotation, Sakurai, spin, temperature 2 Comments

the angular momentum has 2 kinds – orbital angular momentum $L$ , which is caused by a charged particle executing orbital motion, since there are 3 dimension space. and spin $S$ , which is an internal degree of freedom to let particle “orbiting” at there.

thus, a general quantum state for a particle should not just for the spatial part and the time part. but also the spin, since a complete state should contains all degree of freedom.

$\left| \Psi \right> = \left| x,t \right> \bigotimes \left| s \right>$

when we “add” the orbital angular momentum and the spin together, actually, we are doing:

$J = L \bigotimes 1 + 1 \bigotimes S$

where the 1 with L is the identity of the spin-space and the 1 with S is the identity of the 3-D space.

the above was discussed on J.J. Sakurai’s book.

the mathematics of $L$ and $S$ are completely the same at rotation operator.

$R_J (\theta) = Exp( - \frac {i}{\hbar} \theta J)$

where $J$ can be either $L$ or $S$ .

the $L$ can only have effect on spatial state while $S$ can only have effect on the spin-state. i.e:

$R_L(\theta) \left| s \right> = \left| s\right>$

$R_S(\theta) \left| x \right> = \left| x\right>$

the $L_z$ can only have integral value but $S_z$ can be both half-integral and integral. the half-integral value of $Sz$ makes the spin-state have to rotate 2 cycles in order to be the same again.

thus, if the different of $L$ and $S$ is just man-made. The degree of freedom in the spin-space is actually by some real geometry on higher dimension. and actually, the orbital angular momentum can change the spin state:

$L \left| s \right> = \left | s' \right > = c \left| s \right>$

but the effect is so small and

$R_L (\theta) \left| s\right > = Exp( - \frac {i}{\hbar} \theta c )\left| s \right>$

but the c is very small, but if we can rotate the state for a very large angle, the effect of it can be seen by compare to the rotation by spin.

$\left < R_L(\omega t) + R_S(\omega t) \right> = 2 ( 1+ cos ( \omega ( c -1 ) t)$

the experiment can be done as follow. we apply a rotating magnetic field at the same frequency as the Larmor frequency. at a very low temperature, the spin was isolated and $T_1$ and $T_2$ is equal to $\infty$ . the different in the c will come up at very long time measurement and it exhibit a interference pattern.

if $c$ is a complex number, it will cause a decay, and it will be reflected in the interference pattern.

if we find out this c, then we can reveal the other spacial dimension!

___________________________________

the problem is. How can we act the orbital angular momentum on the spin with out the effect of spin angular momentum? since L and S always coupled.

one possibility is make the S zero. in the system of electron and positron. the total spin is zero.

another possibility is act the S on the spatial part. and this will change the energy level.

__________________________________

an more fundamental problem is, why L and S commute? the possible of writing this

$\left| \Psi \right> = \left| x,t \right> \bigotimes \left| s \right>$

is due to the operators are commute to each other. by why?

if we break down the L in to position operator x and momentum operator p, the question becomes, why x and S commute or p and S commute?

$[x,S]=0 ?$

$[p,S]=0 ?$

$[p_x, S_y] \ne 0 ?$

i will prove it later.

___________________________________

another problem is, how to evaluate the Poisson bracket? since L and S is not same dimension. may be we can write the eigenket in vector form:

$\begin {pmatrix} \left|x, t \right> \\ \left|s\right> \end {pmatrix}$

i am not sure.

___________________________________

For any vector operator, it must satisfy following equation, due to rotation symmetry.

$[V_i, J_j] = i \hbar V_k$ run in cyclic

Thus,

where J is rotation operator. but i am not sure is it restricted to real space rotation. any way, spin is a vector operator, thus

$latex [S_x, L_y] = i \hbar S_z = – [S_y, L_x] $

so, L, S is not commute.

Laplacian in spherical coordinate

January 28, 2011

GoLuckyRyan Basic, Spherical Stuffs hydrogen, ladder operator, Laplacian, momentum, spherical harmonic Leave a comment

the Momentum operator in spherical coordinate

$\nabla^2 = \frac {1}{r^2}\frac {\partial } { \partial r} \left ( r^2 \frac {\partial} {\partial r} \right ) - \frac {1}{r^2} L^2$

where L is the Reduced angular momentum operator. the minus sign is very important for giving a correct sign. the original angular momentum operator J is related by:

$J=\hbar^2 L$

by compare the Laplacian in spherical coordinate, the L is

$L^2 = - \frac {1}{sin(\theta)} \frac {\partial}{\partial \theta} \left( sin(\theta) \frac {\partial}{\partial \theta} \right ) - \frac {1}{sin(\theta)} \frac{\partial^2} {\partial \phi ^2}$

But this complicated form is rather useless, expect you are mathematic madman.

we can start from classical mechanic

$\vec{L} = \vec {r} \times \vec{p}$

$L_x = y \frac {\partial} {\partial z} - z \frac {\partial}{\partial y }$

$L_y = z \frac {\partial} {\partial x} - x \frac {\partial}{\partial z }$

$L_z = x \frac {\partial} {\partial y} - y \frac {\partial}{\partial x }$

with the change of coordinate

$\begin {pmatrix} x \\ y \\ z \end{pmatrix} = \begin {pmatrix} r sin(\theta) cos(\phi) \\ r sin(\theta) sin(\phi) \\ r cos(\theta) \end{pmatrix}$

and the Jacobian Matrix $M_J$ , which is used for related the derivatives.

since

$\frac {\partial}{\partial x} = \frac {\partial r}{\partial x} \frac {\partial} {\partial r} +\frac {\partial \theta}{\partial x} \frac {\partial} {\partial \theta}+\frac {\partial \phi}{\partial x} \frac {\partial} {\partial \phi}$

$\frac {\partial}{\partial y} = \frac {\partial r}{\partial y} \frac {\partial} {\partial r} +\frac {\partial \theta}{\partial y} \frac {\partial} {\partial \theta}+\frac {\partial \phi}{\partial y} \frac {\partial} {\partial \phi}$

$\frac {\partial}{\partial z} = \frac {\partial r}{\partial z} \frac {\partial} {\partial r} +\frac {\partial \theta}{\partial z} \frac {\partial} {\partial \theta}+\frac {\partial \phi}{\partial z} \frac {\partial} {\partial \phi}$

which can be simplify

$\nabla_{(x,y,z)} = M_J^T \nabla_{(r, \theta, \phi )}$

$M_J = \frac {\partial ( r, \theta, \phi) }{\partial (x,y,z)}$

$M_J^{\mu\nu} = \frac {\partial \mu}{\partial \nu}$

then, we have

$L_x = i sin(\phi) \frac {\partial }{\partial \theta} +i cot(\theta) cos(\phi) \frac { \partial }{\partial \phi}$

$L_y =-i cos(\phi) \frac {\partial }{\partial \theta} + i cot(\theta) sin(\phi) \frac { \partial }{\partial \phi}$

$L_z = - i \frac {\partial }{\partial \phi}$

However, even we have the functional form, it is still not good. we need the ladder operator

$L_+ = L_x + i L_y = Exp(i \phi) \left( \frac {\partial }{\partial \theta} + i cot(\theta) \frac { \partial }{\partial \phi} \right)$

$L_- = L_x - i L_y = Exp(-i \phi) \left( \frac {\partial }{\partial \theta} - i cot(\theta) \frac { \partial }{\partial \phi} \right)$

notice that

$L_+^\dagger = L_-$

so, just replacing $i \rightarrow -i$ .

when we looking for the Maximum state of the spherical Harmonic $Y_{max}(\theta, \phi)$

$L_+ Y_{max}(\theta,\phi) = 0 *)$

use the separable variable assumption.

$Y_{max}(\theta, \phi) = \Theta \Phi$

$L_+ \Theta \Phi = 0 = - Exp(i \phi) \left( \frac {d\Theta}{d \theta} \Phi + i cot(\theta) \frac { d\Phi}{d\phi} \right) \Theta$

$\frac {tan(\theta)}{\Theta} \frac { d \Theta} {d \Theta } = - \frac {i}{\Phi} \frac {d \Phi} {d \phi} = m$

the solution is

$Y_{max}(\theta,\phi) = sin^m(\theta) Exp(i m \phi )$

$L^2 Y_{max}(\theta, \phi) = m(m+1) Y_{max}(\theta,\phi)$

an application on Hydrogen wave function is here.

angular momentum operator in matrix form

January 28, 2011

GoLuckyRyan Basic, Spherical Stuffs, theory, Working on angular, momentum 3 Comments

in order to fine out the matrix elements, we just need to know 2 equations

$J_z \left| j,m\right> = m \hbar \left|j,m\right>$

$J_\pm \left| j, m \right>=\hbar \sqrt{ j(j+1) -m ( m\pm 1) } \left |j,m \right >$

The calculation is straight forward, but be careful of the sign.

i define the coefficient :

$K_j(m) = \frac{\hbar}{2} \sqrt {j(j+1) -m(m+1) }$

and the matrix coefficients are:

$J_z ^{\mu\nu} (j) = \hbar (j -\mu +1) \delta_{\mu \nu}$

$J_x ^{\mu\nu} (j) = K_j(j-\mu) \delta_{\mu (\nu-1)}+K_j(j-\nu)\delta_{(\mu-1)\nu}$

$J_y ^{\mu\nu} (j) = -i K_j(j-\mu) \delta_{\mu (\nu-1)}+ i K_j (j-\nu)\delta_{(\mu-1)\nu}$

where

$\mu , \nu = 1,2,...,2j+1$

the Kronecker Delta indicated that only 1st upper and lower diagonal elements are non-zero.

δ_μ(ν-1)means the 1st upper diagonal elements. since ν = μ+1 to make it non-zero.

For example:

$J_x (1) = \frac {\hbar }{2} \begin {pmatrix} 0 & \sqrt {2} & 0 \\ \sqrt{2} & 0 &\sqrt{2} \\ 0 & \sqrt{2} & 0\end{pmatrix}$

$J_x (\frac {3}{2}) = \frac {\hbar }{2} \begin {pmatrix} 0 & \sqrt {3} & 0 & 0 \\ \sqrt{3} & 0 & 2 & 0 \\ 0 & 2 & 0 & \sqrt{3} \\ 0 & 0 & \sqrt{3} & 0 \end{pmatrix}$

To compute $J_y$ , we just need to multiply the upper diagonal with $i$ and the lower diagonal with $- i$ .

The coefficient $K_j(j-\mu)$ is every interesting. if we only look at the first upper diagonal. and take the square of each element.

$J_x(\frac {1}{2}) = 1$

$J_x(1) = \begin{pmatrix} 2 & 2 \end{pmatrix}$

$J_x(\frac{3}{2}) = \begin{pmatrix} 3 & 4 & 3 \end{pmatrix}$

and we use this to form a bigger matrix

$\begin {pmatrix} ... & 5 & 4 & 3 & 2 & 1 \\ ... & 10 & 8 & 6 & 4 & 2 \\ ... & ... & 12 & 9 & 6 & 3 \\ ... & ... & ...& 12 & 8 & 4 \\ ... & ... & ... & ... & 10 & 5 \end {pmatrix}$

if we read from the top right hand corner, and take the diagonal element. we can see that they fit the 1st upper diagonal element of $J_x ( j)$ , if we take square root of each one.

and the pattern are just the multiplication table! How nice~

so, i don’t have to compute for j = 5/2.

$J_x ( \frac{5}{2} ) = \frac {\hbar}{2} \begin {pmatrix} 0 & \sqrt{5} & 0 & 0& 0 & 0 \\ \sqrt{5} & 0 & \sqrt{8} & 0 & 0 & 0 \\ 0 & \sqrt{8} & 0 & \sqrt{9} & 0 & 0 \\ 0 & 0 & \sqrt{9} & 0 & \sqrt{8} & 0 \\ 0& 0 &0 & \sqrt{8} &0 & \sqrt{5} \\ 0 & 0 & 0 & 0 & \sqrt{5} & 0 \end {pmatrix}$

but the physical reason for this trick , i don’t know. for the Pascal triangle, we understand the reason for each element – it is the multiplicity.

In general:

$\displaystyle J_x(L) = \frac{\hbar}{2} \begin{pmatrix} 0 & \sqrt{2L} & 0 & ... & ... & ... \\ \sqrt{2L} & 0 & \sqrt{2(2L-1)} & ... & ... & ... \\ ... & ... & ... & ... & ... \\ ... & ... & ... & ... & \sqrt{r (2L-r+1)} & ... \\ .. & ... & ... & ... & ... \end{pmatrix}$

or the $ij$ element of the matrix is

$\displaystyle [J_x(L)]_{i, i>j} = \frac{\hbar}{2} \sqrt{i(2L-i+1)} \delta_{i+1,j}$

Informations we can extract

January 27, 2011

GoLuckyRyan Basic, no math charge, Cross section, momentum, scattering, spin Leave a comment

in scattering experiment, the raw informations we can know or observe are only few things:

the number of particles counted at particular solid angle. ( when you have a unit sphere, the area on the surface is called solid angle)
The polarization (spin)
charge
energy
momentum (time of flight)

Since the number of particles counted is related to the intensity of the incident beam, the density of the target, the interaction and the differential cross section.

on the other hand, the number of particles counted should be related to intensity of incident beam, density of the target and interaction potential. Thus, the differential cross section is related to the interaction potential.

The polarization can be measured by 2nd scattering of known polarization target. or directly from a polarized primary target. or by a polarized beam.

For a nucleus there are 12 properties, and we can group them into 2, 1 is static properties, another is dynamic properties.

Static properties

intrinsic:

mass
radius
spin
parity

extrinsic:

relative abundance
decay half-live
magnetic dipole
electric quadrapole

Dynamic properties

decay modes
reaction mode
cross section
excited state

Of course, the final goal of nuclear physics is find the Hamiltonian for governing the motion of nuclear matter. Thus, we can base on the intrinsic static properties, to deduced the extrinsic and dynamic properties.

think about in atomic physics, we know the potential, the spin, then we can give out every things, like the radius, parity, decay half-live, cross section, etc….

so, the nuclear Hamiltonian is the KEY to open the door of understanding of nuclear matter.

Larmor Precession (quick)

January 23, 2011

GoLuckyRyan Spherical Stuffs, theory angular, Bohr, frequency, g-factor, gyromagnetic, Larmor, Magnetic, magneton, moment, momentum, positron, precess, rotation, Schrödinger equation, TDSE, TISE 1 Comment

Magnetic moment ( $\mu$ ) :

this is a magnet by angular momentum of charge or spin. its value is:

$\mu = \gamma J$

where $J$ is angular momentum, and $\gamma$ is the gyromagnetic rato

$\gamma = g \mu_B$

Notice that we are using natural unit.

the g is the g-factor is a dimensionless number, which reflect the environment of the spin, for orbital angular momentum, g = 1.

$\mu_B$ is Bohr magneton, which is equal to

$\mu_B = \frac {e} {2 m}$ for positron

since different particle has different mass, their Bohr magneton value are different. electron is the lightest particle, so, it has largest value on Bohr magneton.

Larmor frequency:

When applied a magnetic field on a magnetic moment, the field will cause the moment precess around the axis of the field. the precession frequency is called Larmor frequency.

the precession can be understood in classical way or QM way.

Classical way:

the change of angular momentum is equal to the applied torque. and the torque is equal to the magnetic moment cross product with the magnetic field. when in classical frame, the angular momentum, magnetic moment, and magnetic field are ordinary vector.

$\vec {\Gamma}= \frac { d \vec{J}}{dt} = \vec{\mu} \times \vec{B} = \gamma \vec {J} \times \vec{B}$

solving gives the procession frequency is :

$\omega = - \gamma B$

the minus sign is very important, it indicated that the J is precessing by right hand rule when $\omega >0$ .

QM way:

The Tim dependent Schrödinger equation (TDSE) is :

$i \frac {d}{d t} \left| \Psi\right> = H \left|\Psi\right>$

H is the Hamiltonian, for the magnetic field is pointing along the z-axis.

$H = -\mu \cdot B = - \gamma J\cdot B = -gamma B J_z = \omega J_z$

the solution is

$\left|\Psi(t) \right> = Exp( - i \omega t J_z) \left| \Psi(0) \right>$

Thus, in QM point of view, the state does not “rotate” but only a phase change.

However, the rotation operator on z-axis is

$R_z ( \theta ) = Exp( - i \frac {\theta}{\hbar} J_z )$

Thus, the solution can be rewritten as:

$\left|\Psi (t)\right> = R_z( \omega t) \left|\Psi(0)\right>$

That makes great analogy on rotation on a real vector.

on the sum of 4 momentum and excited mass

January 17, 2011

GoLuckyRyan Basic, relativity decay, momentum, natural unit Leave a comment

when we have a decay process, there are many fragments, we can measure their momentum and energy and construct the 4-momentum

$\vec {P_i} = ( E_i , p_i )$

we use the c = 1 unit as usual.

to find out the mass before the decay, we can use

$\sum E_i^2 - \sum p_i^2 = m_{excite}^2$

the reason for the term “excited mass”, we can see by the following illustration.

consider a head on collision of 2 particles in C.M. frame, with momentum p and energy E1 and E2.

the mass for each one is given by

$m_1 = \sqrt {E_1^2 - p^2 }$

$m_2 =\sqrt {E_2^2 - p^2 }$

but if we use the sum of the 4 momentum and calculate the mass,

$\sqrt { (E_1 +E_2)^2 - (p - p)^2} = E_1+E_2$

which is not equal to

$\sqrt { E_1^2 - p^2} + \sqrt{E_2^2 - p^2 }$

in fact, it is larger.

the reason for its larger is, when using the sum of 4 momentum, we actually assumed the produce of collision is just 1 particles, and the collision is inelastic. Thus, if we think about the time-reverse process, which is a decay, thus, some of the mass will convert to K.E. for the decay product.

Hydrogen Atom (Bohr Model)

December 28, 2010

GoLuckyRyan atomic, Basic angular, Coulomb, hydrogen, Laplacian, momentum, normalization, Schrödinger equation, TISE Leave a comment

OK, here is a little off track. But that is what i were learning and learned. like to share in here. and understand the concept of hydrogen is very helpful to understand the nuclear, because many ideas in nuclear physics are borrow from it, like “shell”.

The interesting thing is about the energy level of Hydrogen atom. the most simple atomic system. it only contains a proton at the center, um.. almost center, and an electron moving around. well, this is the “picture”. the fact is, there is no “trajectory” or locus for the electron, so technically, it is hard to say it is moving!

why i suddenly do that is because, many text books said it is easy to calculate the energy level and spectrum for it. Moreover, many famous physicists said it is easy. like Feynman, Dirac, Landau, Pauli, etc… OK, lets check how easy it is.

anyway, we follow the usual say in every text book. we put the Coulomb potential in the Schrödinger equation, change the coordinate to spherical. that is better and easy for calculation because the coulomb potential is spherical symmetric. by that mean, the momentum operator (any one don’t know what is OPERATOR, the simplest explanation is : it is a function of function.) automatically separated into 2 parts : radial and angular part. The angular part can be so simple that it is the Spherical harmonic.

Thus the solution of the “wave function” of the electron, which is also the probability distribution of the electron location, contains 2 parts as well. the radial part is not so trivial, but the angular part is so easy. and it is just $Y(l,m)$ .

if we denote the angular momentum as L, and the z component of it is Lz, thus we have,

$L^2 Y(l,m) = l(l+1) \hbar^2 Y(l,m)$

$L_z Y(l,m) = m \hbar Y(l,m)$

as every quadratic operator, there are “ladder” operator for “up” and “down”.

$L_\pm Y(l,m) =\hbar \sqrt{l(l+1) - m(m\pm 1)} Y(l,m \pm 1)$

which means, the UP operator is increase the z-component by 1, the constant there does not brother us.

it is truly easy to find out the exact form of the $Y(l,m)$ by using the ladder operator. as we know, The z component of the a VECTOR must have some maximum. so, there exist an $Y(l,m)$ such that

$L_+ Y(l,m) =0$

since there is no more higher z-component.

by solve this equation, we can find out the exact form of $Y(l,m)$ and sub this in to L², we can know $Max(m) = l$ . and apply the DOWN operator, we can fins out all $Y(l,m)$ , and the normalization constant is easy to find by the normalization condition in spherical coordinate, the normalization factor is $sin(\theta)$ , instead of 1 in rectangular coordinate.

$\int_0^\pi \int_0^{2 \pi} Y^*(l',m') Y(l,m) sin(\theta) d\theta d \psi = \delta_{l' l} \delta_{m' m}$

Nuclear Physics 101

Hankel Transform

Momentum distribution From Woods-Saxon potential

a review on Hydrogen’s atomic structure

Bohr model

Fine structure

Hyperfine Structure

Smaller Structure

on angular momentum adding & rotation operator

Laplacian in spherical coordinate

angular momentum operator in matrix form

Informations we can extract

Larmor Precession (quick)

on the sum of 4 momentum and excited mass

Hydrogen Atom (Bohr Model)

Recent Posts

Calendar

Archives

Keywords

# of Visitors

Login