Differential Cross Section III

a single diagram can illustrate everything — the relation between the yield ( the number of particle detected per second in the detector ) and the differential cross section.

the upper drawing is a big view, and the lower one is a zoom-in. the red-circles on the upper drawing are same as the lower one.

From the upper one, the number of particles that scatted by the target and go to direction (θ,φ) is :

the left hand side can be interpolated at follow:

is the number of particle per second per unit area, or the flux.

is the total area of  the cross section that deflect or scatter particle to direction (θ,φ).

The left hand side can also be viewed as :

where the fraction after multiplication is the chance of getting scattered to the direction (θ,φ). ( the requirement of the flux is in HERE. )

and the right hand side is the number of particle detected at direction (θ,φ).

since both and depend on (θ,φ). thus we can differential it and get the angle dependent of these 2.

if we set the detector moving as radius R. thus the detector area is:

Therefore, the number of particles will be detected per second on the detector with some area (= Yield ) is:

finish. Oh, the unit of the differential cross section is barn = , recall that a nucleus radius is about . 

the relation between the differential cross section to the nuclear potential was discussed on HERE.

Differential Cross Section II

Last time, the differential cross section discussion is based on quantum mechanics. This time, i try to explain it will out any math. so, that my mum ask me, i can tell her and make her understand. :)

in a scattering experiment, think about a target, say, a proton fixed in the center, it is positive charged. if another proton coming with some energy. it will get repelled, due to the repulsive nature of Coulomb force of same charge. it should be easy to understand, if the proton coming with high energy, it will get closer to the target, or even enter inside the target.

the repelling angle of the proton is not just depend on the energy it carry, but also on the impact parameter ( we usually call it b , but i like to call it r). the impact parameter is the shortest distance between the target and the line of the moving direction of the proton at long long away.

if the impact parameter is large, the proton miss the target. it almost cannot feel the target affection. thus, it go straight and unaffected. when the r is zero, it will hit the target head on head. and due to the repulsion. it will return back.  so, we can understand. the smaller the impact parameter, the deflection will be larger. since it can feel the force stronger.

For same impact parameter, the higher energy proton will have less deflection, since it travel faster, spend less time by the force, and the deflection get less.

Thus, we have an idea that the angle of deflection is high for small impact parameter and high energy. And most important, it only depends on these 2 factors and the effect from the target.

since our detector can only detect some small angle over some small area. So, we can place out detector on some angle, get the yield, and this is the name –  differential cross section come from.

Now, we have a uniform flow of particle with energy E. they will be deflected by the target and go to some angles. If we detect at the deflection angle, see how many particles ( the yield ) we can get in each angle. we can calculate back the effect of the target. For example, for a small angle, the particle get little defected, and this means the particle is from large impact parameter. for a large angle, the particles are from small impact parameter.

In some cases, the number of particle detected will be very high at some particular angle then others angles and this means, the cross section is large. and this means something interesting.

Moreover, don’t forget we can change the energy of the beam. for some suitable energy, the particle will being absorbed or resonance with the target. that given us low or high cross section on the energy spectrum.

( the graph is an unauthorized from the link: http://www.astm.org/Standards/E496.htm )

The above diagram is the differential cross section obtained from a Deuteron to a Tritium ( an isotope of Hydrogen with 2 neutrons and 1 proton) target, and the reaction change the Tritium into Helium and a neutron get out.

The reaction notation is

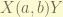
where a is incident particle, X is target, b is out come particle, and Y is the residual particle.

the horizontal axis is detector angle at lab-frame. and the vertical axis is energy of Tritium. we always neglect the angle 0 degree, because it means no deflection and the particle does not “see” the target. at low energy, the d.c.s. is just cause by Coulomb force. but when the energy gets higher and higher, there is a peak around 60 degree. this peak is interesting, because it penetrated into the Helium and reveal the internal structure of it. it tells us, beside of the Coulomb force, there are another force inside. that force make the particle deflects to angle 60 degree. for more detail analysis, we need mathematic. i wish someday, i can explain those mathematics in a very simple way.

Therefore, we can think that, for higher energy beam, the size we can “see” will be smaller. if we think a particle accelerator is a microscope. higher energy will have larger magnification power. That’s why we keep building large and larger machines.

First experiment of 6He with a polarized proton target

DOI : 10.1140/epjad/i2005-06-110-5

this paper reported a first spin polarized proton solid target under low magnetic field ( 0.08 T ) and hight temperature ( 100K )

the introduction overview the motivation of a solid target.

• a polarized gas target is ready on many nuclear experiment.
• on the radioactive beam ( IR beam ), the flux of a typical IR beam is small, since it is produced by 2nd scattering.
  • a low flux on low density makes the experiment almost impossible.
• a solid target has highest density of solid.
  • most solid target can only be polarized on low temperature ( to avoid environmental interaction to reduced the polarization )
    • increase the experimental difficult, since a low temperature should be applied by a cold buffer gas.
  • high field ( the low gyromagnetic  ratio ).
    • high magnetic field make low energy scattered proton cannot get out from the magnetic field and not able to detect.
• a solid target can be polarized at high temperature and low magnetic field is very useful

the material on use is a crystal of naphthalene doped with pentacene.

the procedure of polarizing the proton is :

1. use optical pumping the polarize the electron of pentacene
   • the population of the energy states are independent of temperature and magnetic field.
2. by Dynamic Nuclear Polarization (DNP) method  to transfer  the polarization of the electron to the proton.
   • if the polarization transfer is 100% and the relaxation time is very long. the expected polarization of proton will be 72.8%

The DNP method is archived under a constant microwave frequency with a sweeping magnetic field. when the magnetic field and  microwave frequency is coupled. the polarization transfer will take place.

the next paragraph talks about the apparatus’s size and dimension, in order to fit the scattering experiment requirements.

the polarization measurement is on a scattering experiment with 6He at 71 MeV per nucleons. By measuring the polarization asymmetry , which is related to the yield. and it also equal to the polarization of the target  times the analyzing power .

with a reasonable guess of the target polarization. the analyzing power of  6He was found.

the reason why the polarization-asymmetry is not equal to the analyzing power is that, the target is not 100% polarized, where the analyzing power is defined. when the polarization of the target is 100%, both are the same.

in the analysis part. it used optical model and Wood-Saxon central potential to simulate the result. And compare the result from 6He to 6Li at same energy. the root mean square of 6Li is larger then 6He. it suggest the d-α core of 6Li may responsible for that.

they cannot go further discussion due to the uncertainly on the polarization of the target.

Differential Cross Section

In nuclear physics, cross section is a raw data from experiment. Or more precisely differential cross section, which is some angle of the cross section, coz we cannot measure every scatter angle and the differential cross section gives us more detail on how the scattering going on.

The differential cross section (d.s.c.) is the square of the scattering amplitude of the scatter spherical wave, which is the Fourier transform of the density.

Where the angle θ come from the momentum change. So, sometime we will see the graph is plotted against momentum change instead of angle.

By measuring the yield of different angle. Yield is the intensity of scattered particle. We can plot a graph of the Form factor, and then find out the density of the nuclear or particle.

However, the density is not in usual meaning, it depends on what kind of particle we are using as detector. For example, if we use electron, which is carry elected charge, than it can feel the coulomb potential by the proton and it reflected on the “density”, so we can think it is kind of charge density.

Another cross section is the total cross section, which is sum over the d.s.c. in all angle. Thus, the plot always is against energy. This plot give us the spectrum of the particle, like excitation energy, different energy levels.